CHES2015 Writeup
Intro
On https://ches15challenge.com/ four challenges were made available on 23/06/2015 21:00 CET and the CTF was open for 81 days till 13/09/2015 8:00 CET, first day of the CHES2015 conference.
A backup is available here but the third challenge is online and needs the corresponding server to be up and running.
The Challenge is composed of 4 sub-challenges, which can be solved in any order. Each comes with at least one ciphertext, which contains a secret flag. Except if stated otherwise by the challenge itself, the ciphertext has been obtained thanks to an AES128 encryption in CBC mode with a null initialization vector. An intermediate flag can also appear during the resolution.
Archive: /tmp/t/CHES15Challenge.zip
Length Method Size Cmpr Date Time CRC-32 Name
-------- ------ ------- ---- ---------- ----- -------- ----
0 Stored 0 0% 2015-06-19 17:06 00000000 CHES15Challenge/
0 Stored 0 0% 2015-05-11 13:28 00000000 CHES15Challenge/Challenge1/
128 Defl:N 87 32% 2015-05-05 16:49 dd1dd15e CHES15Challenge/Challenge1/ctxt1.txt
17222400 Defl:N 14839121 14% 2015-05-09 02:45 ab195da9 CHES15Challenge/Challenge1/slowed.wav
0 Stored 0 0% 2015-05-11 13:45 00000000 CHES15Challenge/Challenge2/
326554 Defl:N 221223 32% 2015-05-05 16:14 e875231b CHES15Challenge/Challenge2/Cseh.jpg
128 Defl:N 85 34% 2015-05-05 16:59 adaa02b8 CHES15Challenge/Challenge2/ctxt2.txt
0 Stored 0 0% 2015-06-20 11:22 00000000 CHES15Challenge/Challenge3/
1634 Defl:N 719 56% 2015-06-11 16:27 b94132f8 CHES15Challenge/Challenge3/client.c
128 Defl:N 86 33% 2015-05-05 17:14 a0a61997 CHES15Challenge/Challenge3/ctxt3a.txt
138720144 Stored 138720144 0% 2015-06-23 18:15 2fb47af4 CHES15Challenge/Challenge3/ctxt3b
0 Stored 0 0% 2015-06-23 13:51 00000000 CHES15Challenge/Challenge4/
128 Defl:N 86 33% 2015-05-14 19:35 b85ff4eb CHES15Challenge/Challenge4/ctxt4.txt
16975387 Defl:N 12560569 26% 2015-06-23 13:49 374b4ba4 CHES15Challenge/Challenge4/rom.png
-------- ------- --- -------
173246631 166342120 4% 14 files
Challenge 1
128 May 5 16:49 ctxt1.txt 17222400 May 9 02:45 slowed.wav
First step
Playing slowed.wav gives some unpleasant repetitive noise and a slowed-down voice.
Let's accelerate it:
sox slowed.wav fast.wav speed 3.2
We now hear a text-to-speech voice spelling some letters. It's quite painful to understand them all. Using Audacity to replay easily some parts was helpful.
This gives something like:
the final flag is hidden in the cryptogram but the first one is hidden in the spectrogram extract and collect all the needles in my voice analyze the curve weight is the model of choice
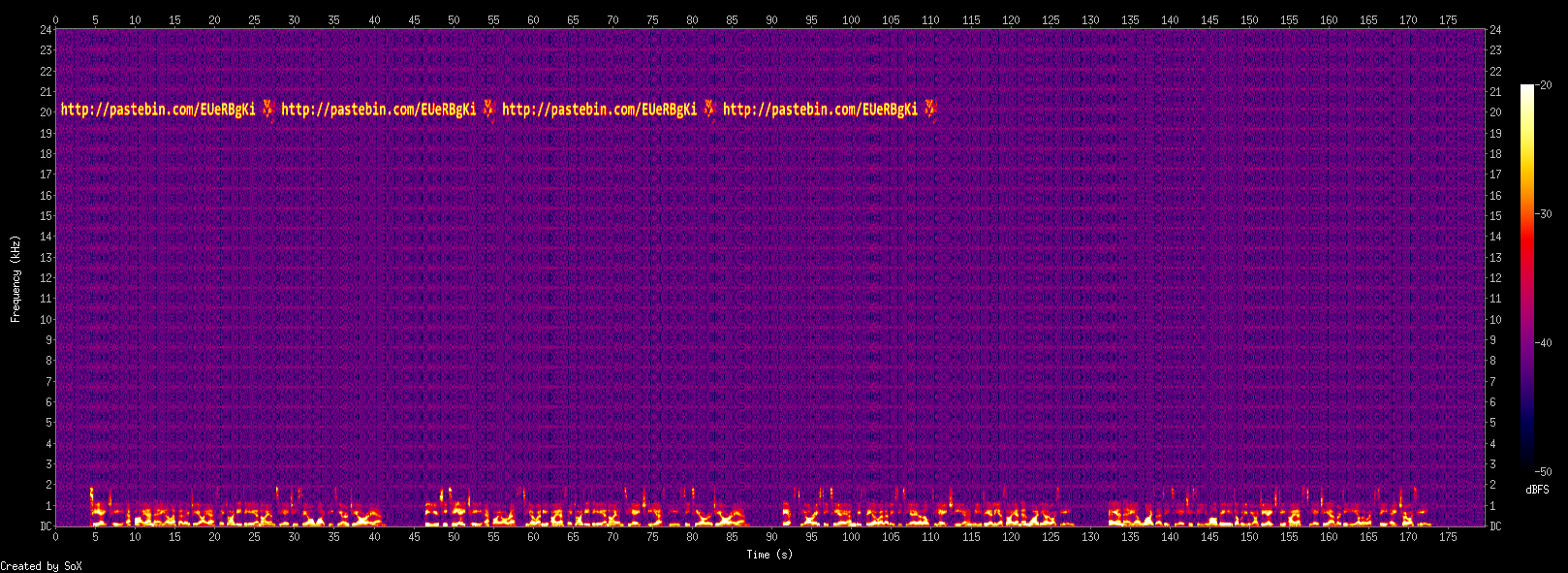
Spectrogram? Ok, let's display it:
sox slowed.wav -n spectrogram
Playing around with the parameters for a better rendering:
sox slowed.wav -n spectrogram -z 30 -Z -20 -x 1600
We get the URL http://pastebin.com/EUeRBgKi with the following content:
Congratulations ! Here is the flag: PaxH7".aoD10+a The audio file also hides 156 successive consumption curves, that you might already have found. The plaintexts used for the generation of these curves are from http://www.maryjones.us/ctexts/a01w.html, without any caps or new lines, encoded in ASCII. 156 blocs of this poem were used (from I to X). As an example, here are the first 25 blocs: gredyf gwr oed g was gwrhyt am di as meirch mwth m (etc)
So the intermediate flag is PaxH7".aoD10+a
Second step
The different hints tell us that there are 156 power traces in the wav and that we should be able to break them with a differential power analysis attack, using the Hamming weight leakage model.
To mount such an attack, one must know which plaintexts were processed, which are here extracted from http://www.maryjones.us/ctexts/a01w.html
Firstly, there are visibly some errors in the 25 blocks described in the pastebin:
- #23 is too short (15 chars)
- #24 is too long (17 chars)
- #25 doesn't match my own processing
- it's not clear if one should use space between chapters or not
I told the organizers who signaled it in their FAQ but, still, attempts to attack the traces (we'll come to that soon) failed.
Actually one has to discard completely the examples and follow the rules: without any caps or new lines so new lines are removed entirely, not replaced by spaces as in the examples.
lynx -dump http://www.maryjones.us/ctexts/a01w.html |\
sed '1,/ *I/d;
/ *[IVX]\+ *$/d;
s/^ *//'|\
tr A-Z a-z|\
tr -d '\n'|\
sed 's/\(................\)/\1\n/g'|\
head -n 156
As you can see the actual plaintexts differ from the example already at the second line:
gredyf gwr oed g wasgwrhyt am dia smeirch mwth myn gvrasa dan vordw (etc)
Later, the FAQ was changed to be more explicit:
The plaintext examples given in Challenge1 are wrong. End of lines are not to be replaced by spaces. For illustration, the second plaintext should not start by "was g" but by "wasg".
How to extract the traces from the wav file?
Let's check if it divides nicely:
17222400/156=110400
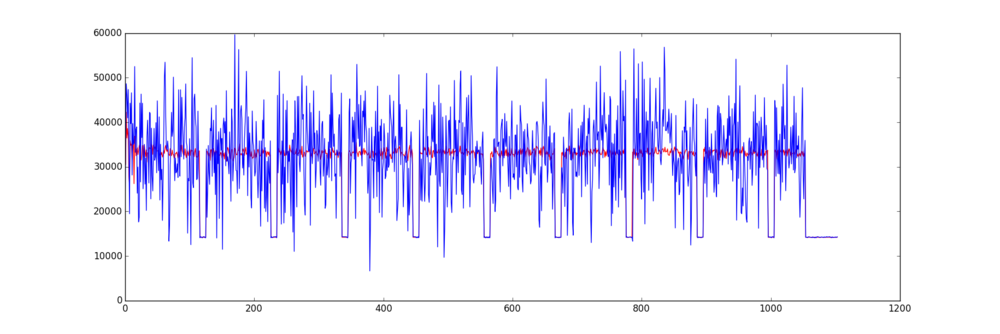
A glimpse at the samples in Audacity reveals that every 50 samples, one sample stands out clearly (the needles):
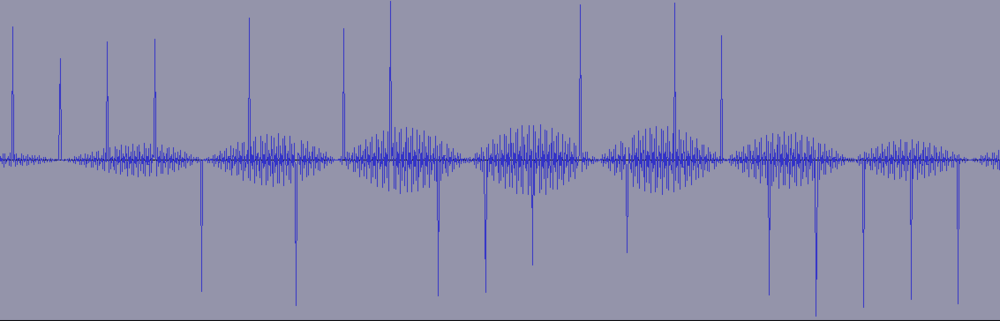
So we decimate the samples by 50 and divide the file in 156 equal chunks.
Some wrapping of the obtained signal suggests that I have to interpret samples as unsigned rather than signed (which makes sense for a power consumption...).
And here is the result, in blue the first trace and in red the average of all traces, showing that they're nicely aligned with a gap between rounds:
Here is a Python script to extract the traces and perform a CPA based on Hamming weight of the S-box outputs in Round 1 of an AES encryption.
#!/usr/bin/env python
# Philippe Teuwen
from numpy import *
import struct
import matplotlib.pyplot as plt
with open("a01w.txt", "rb") as ptf:
plaintexts=array(ptf.read().split('\n'))
bps=2 # 2 bytes per sample
decim=50
# Nr of traces
ntraces=156
# Nr of samples
nsamples=110400/bps/decim
traces=zeros([ntraces, nsamples])
with open('../slowed.wav', 'rb') as wav:
for i in range(ntraces):
for j in range(nsamples):
traces[i,j],=struct.unpack("<H",wav.read(bps*decim)[-2:])
# If one wants to observe the traces, here the first one and the average of all traces:
#plt.plot([average(t) for t in transpose(traces)], 'r')
#plt.plot(traces[0],'b')
#plt.show()
# Usually we truncate traces to target first round which ends around sample 124
# but those traces are so small we don't care
SBOX = [0x63, 0x7c, 0x77, 0x7b, 0xf2, 0x6b, 0x6f, 0xc5, 0x30, 0x01, 0x67,
0x2b, 0xfe, 0xd7, 0xab, 0x76, 0xca, 0x82, 0xc9, 0x7d, 0xfa, 0x59,
0x47, 0xf0, 0xad, 0xd4, 0xa2, 0xaf, 0x9c, 0xa4, 0x72, 0xc0, 0xb7,
0xfd, 0x93, 0x26, 0x36, 0x3f, 0xf7, 0xcc, 0x34, 0xa5, 0xe5, 0xf1,
0x71, 0xd8, 0x31, 0x15, 0x04, 0xc7, 0x23, 0xc3, 0x18, 0x96, 0x05,
0x9a, 0x07, 0x12, 0x80, 0xe2, 0xeb, 0x27, 0xb2, 0x75, 0x09, 0x83,
0x2c, 0x1a, 0x1b, 0x6e, 0x5a, 0xa0, 0x52, 0x3b, 0xd6, 0xb3, 0x29,
0xe3, 0x2f, 0x84, 0x53, 0xd1, 0x00, 0xed, 0x20, 0xfc, 0xb1, 0x5b,
0x6a, 0xcb, 0xbe, 0x39, 0x4a, 0x4c, 0x58, 0xcf, 0xd0, 0xef, 0xaa,
0xfb, 0x43, 0x4d, 0x33, 0x85, 0x45, 0xf9, 0x02, 0x7f, 0x50, 0x3c,
0x9f, 0xa8, 0x51, 0xa3, 0x40, 0x8f, 0x92, 0x9d, 0x38, 0xf5, 0xbc,
0xb6, 0xda, 0x21, 0x10, 0xff, 0xf3, 0xd2, 0xcd, 0x0c, 0x13, 0xec,
0x5f, 0x97, 0x44, 0x17, 0xc4, 0xa7, 0x7e, 0x3d, 0x64, 0x5d, 0x19,
0x73, 0x60, 0x81, 0x4f, 0xdc, 0x22, 0x2a, 0x90, 0x88, 0x46, 0xee,
0xb8, 0x14, 0xde, 0x5e, 0x0b, 0xdb, 0xe0, 0x32, 0x3a, 0x0a, 0x49,
0x06, 0x24, 0x5c, 0xc2, 0xd3, 0xac, 0x62, 0x91, 0x95, 0xe4, 0x79,
0xe7, 0xc8, 0x37, 0x6d, 0x8d, 0xd5, 0x4e, 0xa9, 0x6c, 0x56, 0xf4,
0xea, 0x65, 0x7a, 0xae, 0x08, 0xba, 0x78, 0x25, 0x2e, 0x1c, 0xa6,
0xb4, 0xc6, 0xe8, 0xdd, 0x74, 0x1f, 0x4b, 0xbd, 0x8b, 0x8a, 0x70,
0x3e, 0xb5, 0x66, 0x48, 0x03, 0xf6, 0x0e, 0x61, 0x35, 0x57, 0xb9,
0x86, 0xc1, 0x1d, 0x9e, 0xe1, 0xf8, 0x98, 0x11, 0x69, 0xd9, 0x8e,
0x94, 0x9b, 0x1e, 0x87, 0xe9, 0xce, 0x55, 0x28, 0xdf, 0x8c, 0xa1,
0x89, 0x0d, 0xbf, 0xe6, 0x42, 0x68, 0x41, 0x99, 0x2d, 0x0f, 0xb0,
0x54, 0xbb, 0x16]
HW = [bin(n).count("1") for n in range(0,256)]
varray = zeros((ntraces,256,16),uint8)
keys = arange(0,16)
############# Section computing hypotheses #############
# based on https://media.blackhat.com/eu-13/briefings/OFlynn/bh-eu-13-for-cheapstakes-oflynn-slides.pdf
# by Colin O'Flynn, slide #16
#For all 16 bytes of key
for bnum in range(0, 16):
diffs = [0]*256
#For each 0x00..0xFF possible value of the key byte
for key in range(0, 256):
#For each trace, do the following
for tnum in range(len(traces)):
#Generate the output of the SBOX
varray[tnum,key,bnum]=HW[SBOX[ord(plaintexts[tnum][bnum]) ^ key]]
############# Section implementing the CPA attack #############
# based on https://github.com/ermin-sakic/first-order-dpa/blob/master/attack.py
# by Ermin Sakic, under http://www.apache.org/licenses/LICENSE-2.0
#Computing the mean values for the hypothetical plaintext values v (byte-wise)
hammingmeanvalue = zeros((varray[1,:,1].size,16),float32)
for i in range(0,varray[1,:,1].size):
for n in range(0,16):
hammingmeanvalue[i,n] = average(varray[:,i,n])
#Computing the difference to the actual values v
for i in range(0,16):
for n in range(0,256):
varray = varray.astype(float32)
varray[:,n,i] = varray[:,n,i]-hammingmeanvalue[n,i]
#Computing the mean values of the power traces - sample-wise
powermeanvalue = zeros((traces[1,:].size),float32)
for i in range(0,traces[1,:].size):
powermeanvalue[i] = average(traces[:,i])
#Computing the difference to the actual values
meanTraces = traces-powermeanvalue
#Creating the 3-dimensional correlation for all 16 Bytes
rarray = zeros((256,traces[1,:].size,16),float32)
for i in range(0,16):
for j in range(0,256):
rarray[j,:,i] = (dot(varray[:,j,i],meanTraces)) / sqrt(sum(varray[:,j,i]**2, axis=0) * sum(meanTraces**2, axis=0))
#(^2) to get all the positive values
s=rarray[:,:,i]**2
#Find the highest correlation value
keys[i] = nonzero(amax(s) == s)[0]
#################### End of Sections ####################
print ''.join(["%02x" % x for x in keys])
# Testing the recovered key:
from Crypto.Cipher import AES
with open("../ctxt1.txt", "rb") as f:
c = f.read().decode('hex')
aes = AES.new(''.join([chr(x) % x for x in keys]), AES.MODE_CBC, '\x00'*16)
print aes.decrypt(c)
Running it:
./attack.py 074d9bb982d97d63b8c8fbea11bd7180 Congratulations! Here's the final flag for Step1: a1309*!POs/f8s
It appears that using the first 128 traces is enough to recover the key immediately.
Challenge 2
First step
326554 May 5 16:14 Cseh.jpg 128 May 5 16:59 ctxt2.txt
The filename is a bit weird at first sight, Cseh<>Ches ?
Here is Cseh.jpg:
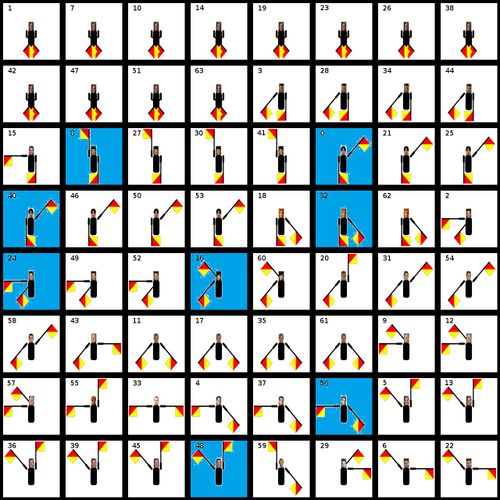
It shows flag semaphore characters, each with a photo of people famous in the crypto community. Hopefully we don't have to recognize them all to complete the challenge ;)
So each character represents a letter from the alphabet and they are sorted alphabetically.
Each square features a number from 0 to 63 and 8 of them are blue.
At this point the grid and the 8 blue squares (8 queens problem??) vaguely makes me thinking of chess game but not much.
Reordering the squares gives:
*E _ H A S T Y _ *D O _ N O T _ B *I N G _ K E Y _ *H E _ D A W D L *G R A N T S _ T *E D _ M A T E _ *T H E _ H E L P *S O L V I N G _
The blue squares line up nicely but the text doesn't make completely sense. It has to be read bottom-up so let's reorder again the grid:
*S O L V I N G _ *T H E _ H E L P *E D _ M A T E _ *G R A N T S _ T *H E _ D A W D L *I N G _ K E Y _ *D O _ N O T _ B *E _ H A S T Y _
Solving the helped mate grants the dawdling key Do not be hasty
Mate? So it has to do with chess in the end? At least counting rows bottom-up is typical of chess notation.
The blue squares now aligned in the first column reveal another word: "steghide", a well known steganography tool developed by Stefan Hetzl.
steghide always takes a passphrase, so let's give it the clue we have:
steghide extract --stegofile Cseh.jpg --passphrase "SOLVING THE HELPED MATE GRANTS THE DAWDLING KEY DO NOT BE HASTY "
We get a file "Gabor.txt" and the intermediate flag:
Intermediate flag: pqq1\du52c:|fA N7/3PP3/4p2p/1P2P3/3p2pP/3p2pb/3P1pnk/5K1n w - - Solution= 51||59||47||39||59||35||AES256-Key AES256-key= ??||??||??||??||??||??||??||??||??||??||??||??||??||??||??||??||??||??||??||??||??||??||??||??||??||??||??||??||??||??||??||??
The remaining is more cryptic, as well as the filename, again: Gabor.
Second step
Googling about Gabor, Cseh and chess reveals that Gabor Cseh is a chess composer, specialist of helpmates, who tragically passed away 15 years ago.
We're on the right track.
A helpmate is a type of chess problem in which both sides cooperate in order to achieve the goal of checkmating Black. In a helpmate in n moves, Black moves first, then White, each side moving n times, to culminate in White's nth move checkmating Black.
Ok that's not really chess but making a puzzle on a chess board with strange rules ;)
N7/3PP3/4p2p/1P2P3/3p2pP/3p2pb/3P1pnk/5K1n w - -
is a starting position encoded in FSN standard notation.
There is an online converter to Wikipedia notation which gives:
{{Chess diagram|=
| tright
|
|=
8 |nl| | | | | | | |=
7 | | | |pl|pl| | | |=
6 | | | | |pd| | |pd|=
5 | |pl| | |pl| | | |=
4 | | | |pd| | |pd|pl|=
3 | | | |pd| | |pd|bd|=
2 | | | |pl| |pd|nd|kd|=
1 | | | | | |kl| |nd|=
a b c d e f g h
|
}}
As I don't have this renderer on my wiki, I simply edited the standard chess diagram Wikipedia page and used the preview to render it.
Here is the result:

It's very close to one of the famous helpmates from Gabor Cseh:
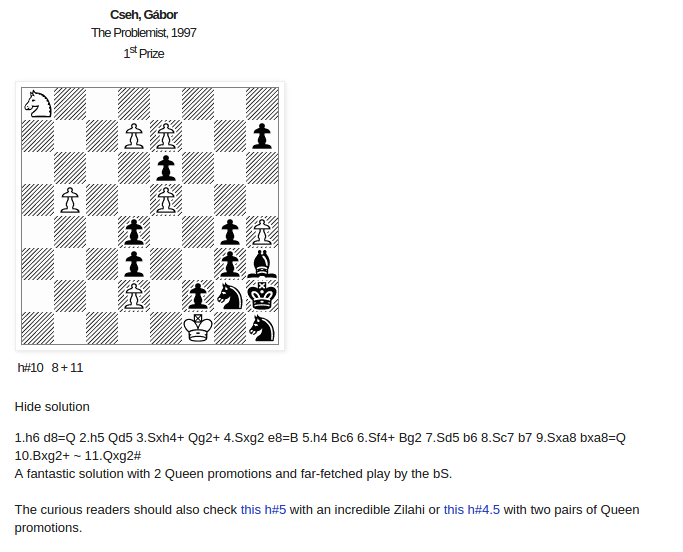
The difference is that the Black did already one move.
Other refs for the record here, here and here
We got the solution, but it's not spelling an AES key yet:
1.h6 d8=Q 2.h5 Qd5 3.Sxh4+ Qg2+ 4.Sxg2 e8=B 5.h4 Bc6 6.Sf4+ Bg2 7.Sd5 b6 8.Sc7 b7 9.Sxa8 bxa8=Q 10.Bxg2+ ~ 11.Qxg2#
It's using the algebraic notation
There exists also a numeric notation but it can't deal with values such as "59".
We know first moves are h6 (already done), d8=Q h5 Qd5 and they should match 51->59 47->39 59->35.
The solution is simply to reuse the notation of our initial reordered square, counting from 0 to 63.
Translating all next moves gives the AES-256 key:
1.h6 already played d8=Q 51 59 2.h5 47 39 Qd5 59 35 3.Sxh4+ 14 31 Qg2+ 35 14 4.Sxg2 31 14 e8=B 52 60 5.h4 39 31 Bc6 60 42 6.Sf4+ 14 29 Bg2 42 14 7.Sd5 29 35 b6 33 41 8.Sc7 35 50 b7 41 49 9.Sxa8 50 56 bxa8=Q 49 56 10.Bxg2+ 23 14 11.Qxg2# 56 14
cat ctxt2.txt |xxd -r -p|openssl enc -d -aes-256-cbc -iv 00000000000000000000000000000000 -K 1431351431145260393160421429421429353341355041495056495623145614 -nopad
Congratulations! Here's the final flag for Step2: 9qp0..-dhs19sA
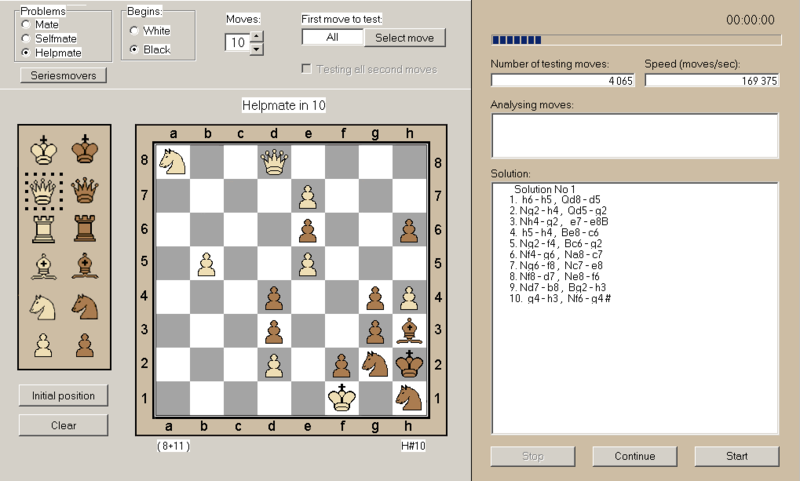
Later @foxTN told me about Chess Explorer v6.3, a Windows program that runs smoothly under Wine too. The trick with Chess Explorer and regular helpmate is that if White is supposed to win, Black should do the first move, which is not the case here. So assuming you didn't find about Gabor Cseh's problem, you have first to understand the initial moves sequence 51->59 47->39 59->35 then e.g. play the first White move to promote Pawn to Queen then encode the board position in Chess Explorer, only then it's able to solve the problem and give the remaining of the sequence:
Challenge 3
1634 Jun 11 16:27 client.c
128 May 5 17:14 ctxt3a.txt
138720144 Jun 23 18:15 ctxt3b
First step
client.c is a little program that contacts IP 5.196.94.96 PORT 1337, no more intelligence on the client side.
gcc -o client client.c
./client
Usage: ./client AES128_ciphertext AES128_ciphertext must be one bloc of 16 bytes. Example: ./client 00112233445566778899aabbccddeeff
./client 00112233445566778899aabbccddeeff
Deciphering request recorded: 00112233445566778899aabbccddeeff Authentication required. Generating p... /-//------//--------//-//---//------ (lengthy stream, cut for readability) OK! Generating q... /---//--//-//------------------//--- (lengthy stream, cut for readability) OK! Generating exponents... OK! Public RSA Modulus N=2819689676488421872318870471104347523394155784102180638192285162391561217 7002285110448907284975469577470042981032214712077436006374273453665129408493100492119974988320 6211522606167656086081447613592593266115164965469369723373725568734890642591586543302333084235 507671120584710284562298067137385662842168426203 Public RSA Exponent e=167919316235161637592329487918880523067209258876972194711854520844130725 28496181482955857814936477791630898151127677357783836901437936391906579743197325527 Please prove your authorization by signing the following number: 2586133324520058154902975298143797583539778758236125175238003940853319737887332403647260804369 6936870393136937923280064885316920458913898712173041186513571902234826172382108074766731928787 3994921666750148840845768163411337299144187778246260686850240562440647168110450270539072672942 538758463414163993430703442 Signature?
Then you can type in a number and it'll go on:
Deciphering AES ciphertext... 10 9 8 7 6 5 4 3 WARNING!!!!!!!!!! WRONG AUTHENTICATION!!UNAUTHORIZED ACCESS! 2 1 Plaintext=57d32bc8be00ac2e291a0a5ba657ce98
Every new attempt leads to new data.
So based on the info we get, we've to break the freshly generated 1024-bit RSA key and sign the challenge.
All the data shown while generating p and q seem to indicate that it could be used as side-channel info to recover p and q.
But after some poor attempts I wanted to try another simpler attack: the Common Factor attack, which is very well explained here.
So firstly I collected a few N.
Sending non-interactively the signature in bash wasn't that trivial:
python -c "print '0' * 123"|nc 5.196.94.96 1337
Sending less than 1024 bytes wasn't enough, the server was still asking for signature.
Sending between 1024 and 2046 did the job
Above 2046 -> crash before requesting the signature, ooops :-) Going further on that part is forbidden by the rules so...
#!/bin/bash
for ((i=0;i<1000;i++)); do
python -c "print '0' * 1024"|nc 5.196.94.96 1337|grep -a N=|sed 's/.*N=//'|tee -a N.log
done
cat N.log |sort|uniq > Nuniq.log
Then try to find common factors between them:
#!/usr/bin/env python
from fractions import gcd
with open('Nuniq.log', 'rb') as f:
table=f.read().split('\n')
table=[int(x.rstrip('\x00')) for x in table[:-1]]
for i in range(len(table)-1):
for j in range(i+1, len(table)):
if gcd(table[i], table[j]) != 1:
print i, j, gcd(table[i], table[j]), '\n'
./gcd.py|tee factors
0 1 13467571150670687066957875085721965877832239113551705444143019591603700515153235000428172641836606112908781752701461471841368993247989009896064991510937251 0 15 13522691794376224089868859278287899501033018902746299241330282162167180595895681147672319399654497784997302521749226127494937660644522050195279028737986711 0 16 13467571150670687066957875085721965877832239113551705444143019591603700515153235000428172641836606112908781752701461471841368993247989009896064991510937251 0 48 13467571150670687066957875085721965877832239113551705444143019591603700515153235000428172641836606112908781752701461471841368993247989009896064991510937251 0 59 13467571150670687066957875085721965877832239113551705444143019591603700515153235000428172641836606112908781752701461471841368993247989009896064991510937251
Indeed, bingo, some common factors are found which means the corresponding keys can be factorized!
Let's verify one of the broken keys:
#!/usr/bin/env python
import gmpy2
def inv_mod(a,n):
return long(gmpy2.invert(a,n))
N=489683129743306941322805095882419224736370814718392548211121787339898087617026431386163546699159846569409239636639246361955291658228707241672498393344940245746337087380408795944103457949933554475592737732728331538286128796839639612626004010652921226752995071610898329413586369760403997380285336731265742419107
e=22128785094155235645734655029153146544996333536428633068744601079808079739933367737532667883249081632568925074568802041762302172470324152703276601897434961
m=441987425702747774855681247465818753113679086591585255820825141069742825411397383716271603205540116590744218129104195126848983890799758912319781831522483360139502987422581260021027022403585155205768233230249123576372864027163253266915275272384323839767364430629154149984119201559268565332381649157195585848765
p=21563957808398119329545349513312897291720371794644161565433575994922624494866014735925135594671402533520230648695949559828278766299067426136066601816643711
q=22708406967509416561081471369947020796745437757938294005271339336356008357234294069698063747451399564794968797317330497407167861251551902204973484175503837
assert p*q==N
phi=(p-1)*(q-1)
d=inv_mod(e,phi)
assert (e*d)%phi==1
sign=pow(m,d,N)
assert pow(sign,e,N)==m
Everything runs smoothly.
Now time to write a full attack:
#!/usr/bin/env python
import sys
import socket
import random
from fractions import gcd
def log(m):
with open('log.txt', 'ab') as log:
log.write(m)
def verbose(m):
pass
# print m
import gmpy2
def inv_mod(a,n):
return long(gmpy2.invert(a,n))
Ntable=[]
def fact(N):
for n in Ntable:
if N==n:
return False
if gcd(n, N) != 1:
p=gcd(n, N)
q=N/p
Ntable.append(N)
return (p,q)
Ntable.append(N)
return False
TCP_IP = "5.196.94.96"
TCP_PORT = 1337
BUFFER_SIZE = 1024
with open('ctxt3a.txt', 'rb') as f:
ciphertext=f.read()
ivs='00'*16+ciphertext
for ci in range(0,len(ciphertext),32):
c=ciphertext[ci:ci+32]
iv=ivs[ci:ci+32]
decoded=False
print iv, '+', c
while not decoded:
print '.',
sys.stdout.flush()
try:
s = socket.socket(socket.AF_INET, socket.SOCK_STREAM)
s.settimeout(5.0)
s.connect((TCP_IP, TCP_PORT))
s.send(c)
log("\nSEND "+c)
data = ""
watch1="Modulus N="
watch2="\n\nPublic RSA Exponent e="
watch3="\n\nPlease prove your authorization by signing the following number:\n"
watch4="\n\nSignature?"
data=""
while watch4 not in data:
dd = s.recv(BUFFER_SIZE)
log(dd)
data += dd
N=int(data[data.index(watch1)+len(watch1):data.index(watch2)].rstrip('\x00'))
f=fact(N)
if f:
print '!'
sys.stdout.flush()
verbose("N=%i" % N)
p,q=f
e=int(data[data.index(watch2)+len(watch2):data.index(watch3)].rstrip('\x00'))
verbose("e=%i" % e)
m=int(data[data.index(watch3)+len(watch3):data.index(watch4)].rstrip('\x00'))
verbose("m=%i" % m)
phi=(p-1)*(q-1)
# d, the modular multiplicative inverse of e (mod phi(n))
d=inv_mod(e,phi)
sign=pow(m,d,N)
verbose("p=%i" % p)
verbose("q=%i" % q)
verbose("phi=%i" % phi)
verbose("d=%i" % d)
verbose("sign=%i" % sign)
s.send("%i" % sign)
log("\nSEND ")
log("%i" % sign)
watch="Plaintext="
data=""
while watch not in data:
dd = s.recv(BUFFER_SIZE)
log(dd)
data += dd
if "Authentication complete" not in data:
print "FAILED??"
verbose(data)
continue
plain=data[data.index(watch)+len(watch):].rstrip('\x00').rstrip('\x00\n')
plain="".join([chr((ord(x)) ^ (ord(y))) for (x,y) in zip(plain.decode('hex'), iv.decode('hex'))])
print plain
decoded=True
s.close()
except ZeroDivisionError:
print "Error captured"
./client.py
00000000000000000000000000000000 + bddb6ba6569c7e079c76c48a67c9fc68 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ! Congratulations! bddb6ba6569c7e079c76c48a67c9fc68 + 55bd14dd8ac2a717075a598bed0a986d . ! Here's the firs 55bd14dd8ac2a717075a598bed0a986d + c8b9f818cffc47e214c81e0f3d01d948 . . . . . . . . . . . . . . . . . . . . ! t flag for Step3 c8b9f818cffc47e214c81e0f3d01d948 + fd2de97665d496ba405a304945623ee7 . . ! : 7Pqmd85(8dd)x(
The attack takes 35s on my laptop.
@ddddaveede points out that for larger collections of public keys, you may want to use the fast pairwise GCD implementation available at https://factorable.net/index.html . In our case the network was clearly the bottleneck.
First step, "fox" version
@foxTN found how to take advantage of the stream when p and q are generated.
The attack is described in this paper: A New Side-Channel Attack on RSA Prime Generation (pdf) by Thomas Finke et al. and presented at CHES 2009.
It works if the primes are generated by following this algorithm:
- Prepare a table of the first N odd primes, starting from 3,5,7,11,... (we can drop 2 as we've just to take odd numbers to avoid it)
- Pick a random odd number about the size of the desired prime length
- Perform a quick check if it's divisible by one of the primes from the table
- If yes, add 2 and start over
- If not, then go for a more thorough test of its primality, e.g. the Miller-Rabin primality test
- Again, if it's not prime, add 2 and start over
At the end you get your prime
What we can observe here looks like this:
Generating p... /-//------//--------//-//---//------ (lengthy stream, cut for readability)
Where the streams are each made of about 25000 to 65000 symbols.
Length of "---" segments varies between 1 and 256 so we can guess it's following the algorithm described above:
- Prepare a table of the first 256 odd primes
- Pick a random number about the size of the desired prime length
- Perform a quick check if it's not divisible by 2 or any of the primes of the table, starting from 3,5,7,11,... and output "-" for each successful test
- If one of the test fails (so if it divides), add 1, output "/" and start over
- If all division tests pass, then test more thoroughly its primality
- Again, if it's not prime, add 1, output "/" and start over
- If all tests pass, output "/" and we're done, we found a prime
Looking at the end of a stream, e.g. if it's
...//---//---------------------------------//-//-(*256)/
this means, reading from right to left, that if p is prime, p-2 is divisible by the first element of the prime table: 3, p-4 is divisible by the 33rd: 139, p-6 is divisible by 7, etc
...//---//---------------------------------//-//-(*256)/
divisible, take next: i+=2
try /3: pass
try /5: pass
try /7:
divisible, take next: i+=2
try /3: pass
...
try /139:
divisible, take next: i+=2
try /3:
divisible, take next: i+=2
try /3: pass
...
do a Miller-Rabin test: pass => outputs p
So
- (p-2) mod 3 = 0
- p mod 3 = 2
- (p-4) mod 139 = 0
- p mod 139 = 4
- (p-6) mod 7 = 0
- p mod 7 = 6
- etc.
And of course
- (p-1) mod 2 = 0
- p mod 2 = 1
Then combining all those equations via the Chinese remainder theorem tells us there is a unique solution for p mod (2*3*139*7*...)
If the stream is long enough and we collected enough equations such that the product (2*3*139*7*...) is large enough (paper says about 300 bits for a 1024-bit RSA, so 512-bit p), the solution is p.
Do the same for q then check if p*q==N
The paper goes on to find p and q in case there is less information, but the challenge was apparently made such that the streams were long enough (we get about 500 to 1100 equations per prime and the product is always above 512 bits).
Here is the code of fox' attack:
#!/usr/bin/env python
import sys
import gmpy
from operator import mul
from sympy.ntheory.modular import crt
from socket import socket
def recv_until(s, string):
buf = ""
while not buf.endswith(string):
r = s.recv(1)
buf += r
if len(r) == 0:
print "remote server terminated connection: '%s'" % buf
raise socket.error
exit()
return buf[:-len(string)]
def xor(s1, s2):
return "".join([chr(ord(s1[i]) ^ ord(s2[i])) for i in range(len(s1))])
def chunks(l, n):
"""Yield successive n-sized chunks from l."""
for i in xrange(0, len(l), n):
yield l[i:i+n]
primes = [ 3, 5, 7, 11, 13, 17, 19, 23, 29,
31, 37, 41, 43, 47, 53, 59, 61, 67, 71,
73, 79, 83, 89, 97, 101, 103, 107, 109, 113,
127, 131, 137, 139, 149, 151, 157, 163, 167, 173,
179, 181, 191, 193, 197, 199, 211, 223, 227, 229,
233, 239, 241, 251, 257, 263, 269, 271, 277, 281,
283, 293, 307, 311, 313, 317, 331, 337, 347, 349,
353, 359, 367, 373, 379, 383, 389, 397, 401, 409,
419, 421, 431, 433, 439, 443, 449, 457, 461, 463,
467, 479, 487, 491, 499, 503, 509, 521, 523, 541,
547, 557, 563, 569, 571, 577, 587, 593, 599, 601,
607, 613, 617, 619, 631, 641, 643, 647, 653, 659,
661, 673, 677, 683, 691, 701, 709, 719, 727, 733,
739, 743, 751, 757, 761, 769, 773, 787, 797, 809,
811, 821, 823, 827, 829, 839, 853, 857, 859, 863,
877, 881, 883, 887, 907, 911, 919, 929, 937, 941,
947, 953, 967, 971, 977, 983, 991, 997, 1009, 1013,
1019, 1021, 1031, 1033, 1039, 1049, 1051, 1061, 1063, 1069,
1087, 1091, 1093, 1097, 1103, 1109, 1117, 1123, 1129, 1151,
1153, 1163, 1171, 1181, 1187, 1193, 1201, 1213, 1217, 1223,
1229, 1231, 1237, 1249, 1259, 1277, 1279, 1283, 1289, 1291,
1297, 1301, 1303, 1307, 1319, 1321, 1327, 1361, 1367, 1373,
1381, 1399, 1409, 1423, 1427, 1429, 1433, 1439, 1447, 1451,
1453, 1459, 1471, 1481, 1483, 1487, 1489, 1493, 1499, 1511,
1523, 1531, 1543, 1549, 1553, 1559, 1567, 1571, 1579, 1583,
1597, 1601, 1607, 1609, 1613, 1619, 1621]
cipher = open("./ctxt3a.txt").read().decode('hex')
iv = '\x00'*16
counter = 0
for chunk in chunks(cipher, 16):
while True:
s = socket()
s.connect(("5.196.94.96", 1337))
s.send(chunk.encode('hex') + "\n")
content = recv_until(s, "?")
p = content.split("\n")[4]
q = content.split("\n")[8]
n = int(content.split("\n")[14].split("=")[1].replace("\x00", ""))
e = int(content.split("\n")[16].split("=")[1].replace("\x00", ""))
to_sign = int(content.split("\n")[19].replace("\x00", ""))
primes_p = [len(x.replace("/", "")) for x in p.split("//")]
primes_q = [len(x.replace("/", "")) for x in q.split("//")]
Sp = [2]
Sp_v = [1]
for i, p_idx in enumerate(primes_p):
p_idx = int(p_idx)
if p_idx == 256:
continue
Sp.append(primes[p_idx-1])
Sp_v.append(2*(len(primes_p) - i - 1))
Sq = [2]
Sq_v = [1]
for i, p_idx in enumerate(primes_q):
p_idx = int(p_idx)
if p_idx == 256:
continue
Sq.append(primes[p_idx-1])
Sq_v.append(2*(len(primes_q) - i - 1))
ap = crt(Sp, Sp_v)[0]
bq = crt(Sq, Sq_v)[0]
p, q = ap, bq
if p * q != n: # FAIL! Retry...
continue
phi = (p-1) * (q-1)
d = gmpy.invert(e, phi)
assert pow(pow(42, e, n), d, n) == 42
resp = pow(to_sign, d, n)
s.send(str(resp))
recv_until(s, "Authentication complete!")
plain = s.recv(1024).split("=")[1].split()[0]
plain = xor(plain.decode('hex'), iv)
iv = chunk
sys.stdout.write(plain)
sys.stdout.flush()
break
print
Congratulations! Here's the first flag for Step3: 7Pqmd85(8dd)x(
The attack takes 3.1s on my laptop.
Retrospectively I think the authors of this challenge intended us to solve it this way because the gaps before finding p and q are abnormally long, which helps a lot this attack.
But to do so, they constrained their set of primes so much that the common factor attack became feasible.
Well, that's just an hypothesis...
I've also the feeling the code on the server changed somewhere like one week after the beginning because there were differences in the network packets and in the streams: at the beginning the last stream segment was always //-(*257)/ while after it was always //-(*256)/
Second step
Second ciphertext: ctxt3b
No extension but the file is large, 135Mb!
If we want to use the same attack to decode the entire file it will take ages.
ctxt3b seems to be also aes-128-cbc encoded (no repetition of blocks) and starts with 16*'\x00', the IV?
Let's decode the first 1500 bytes and analyze the result:
file result result: PC bitmap, Windows 95/NT4 and newer format, 6800 x 6800 x 24
It's a BMP, more details can be seen using e.g. hachoir-wx:
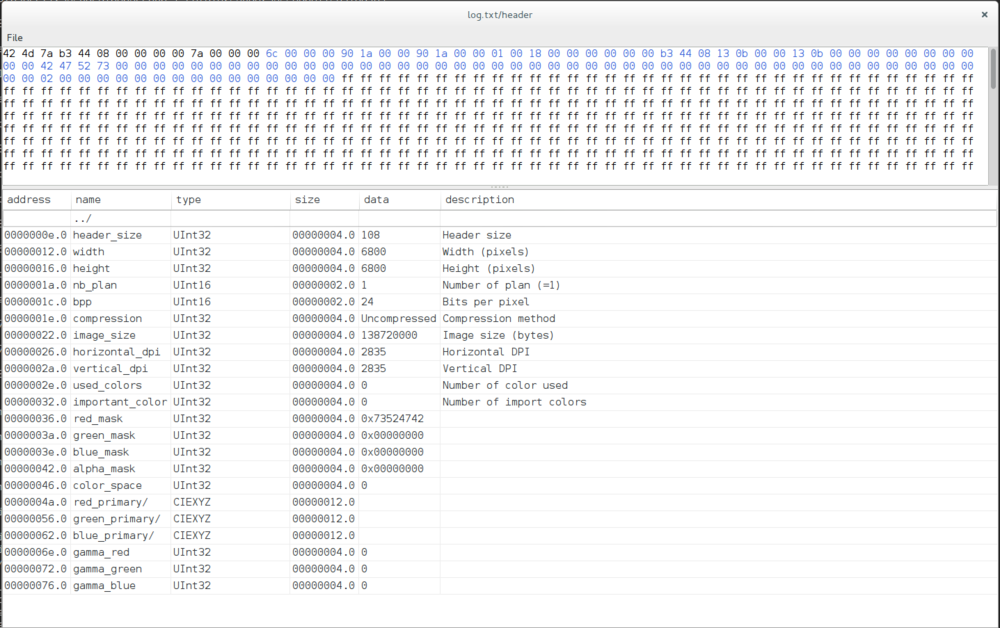
A quick check on the sizes:
0x7a+(6800*6800*3)=138720122 +iv=138720138 +pad=138720144
Ok so there is nothing after the BMP.
BMP is not compressed so we can sample it and we don't have to decrypt it entirely.
Oh wait but it's CBC encrypted, so all blocks are chained, right?
Well it's not much a problem when decrypting, cf PoC||GTFO 0x06 Section 7 and Wikipedia: you just need to XOR with the previous ciphertext block, no chaining.
The tactic will be the following one: complete the decoded header to create an empty BMP, sample randomly the encrypted bmp and paint on our empty BMP.
Here we keep the header and the first 400px (=1200 bytes), then we paint with some pastel green color so we'll be able to see where we're painting on, being in white or in other colors:
#!/usr/bin/env python
with open('decoded_first1500','rb') as h, open('decoded.bmp', 'wb') as b:
b.write(h.read()[:0x7A+3*400])
b.write('\x99\xff\xee'*(6800*6800-400))
The attack code is almost identical to the first step, just the way to select ciphertexts and complete the BMP are different.
We saw "fox" version was faster, but only at the beginning as finding common factors require first to collect some public keys. On the long run both attacks are equivalent for this second step.
#!/usr/bin/env python
import sys
import socket
import random
from fractions import gcd
def log(m):
pass
# with open('log.txt', 'wb') as log:
# log.write(m)
def verbose(m):
pass
# print m
import gmpy2
def inv_mod(a,n):
return long(gmpy2.invert(a,n))
Ntable=[]
def fact(N):
for n in Ntable:
if N==n:
return False
if gcd(n, N) != 1:
p=gcd(n, N)
q=N/p
Ntable.append(N)
return (p,q)
Ntable.append(N)
return False
TCP_IP = "5.196.94.96"
TCP_PORT = 1337
BUFFER_SIZE = 1024
with open('ctxt3b', 'rb') as f:
ciphertext=f.read()
xpos=0
ypos=0
width=6800
height=6800
# flag coordinates:
#xpos=1850
#ypos=4100
#width=5100-xpos
#height=4500-ypos
with open('decoded.bmp', 'rb+',0) as bmp:
for i in range(1000000):
ci=(((0x7A+(random.randint(xpos,xpos+width)*3)+(6800-(random.randint(ypos,ypos+height)))*6800*3)/16)+1)*16
c=ciphertext[ci:ci+16].encode('hex')
iv=ciphertext[ci-16:ci].encode('hex')
decoded=False
print iv, '+', c
while not decoded:
print '.',
sys.stdout.flush()
try:
s = socket.socket(socket.AF_INET, socket.SOCK_STREAM)
s.settimeout(5.0)
s.connect((TCP_IP, TCP_PORT))
s.send(c)
log("\nSEND "+c)
data = ""
watch1="Modulus N="
watch2="\n\nPublic RSA Exponent e="
watch3="\n\nPlease prove your authorization by signing the following number:\n"
watch4="\n\nSignature?"
data=""
while watch4 not in data:
dd = s.recv(BUFFER_SIZE)
log(dd)
data += dd
N=int(data[data.index(watch1)+len(watch1):data.index(watch2)].rstrip('\x00'))
f=fact(N)
if f:
print '!'
sys.stdout.flush()
verbose("N=%i" % N)
p,q=f
e=int(data[data.index(watch2)+len(watch2):data.index(watch3)].rstrip('\x00'))
verbose("e=%i" % e)
m=int(data[data.index(watch3)+len(watch3):data.index(watch4)].rstrip('\x00'))
verbose("m=%i" % m)
phi=(p-1)*(q-1)
# d, the modular multiplicative inverse of e (mod phi(n))
d=inv_mod(e,phi)
sign=pow(m,d,N)
verbose("p=%i" % p)
verbose("q=%i" % q)
verbose("phi=%i" % phi)
verbose("d=%i" % d)
verbose("sign=%i" % sign)
s.send("%i" % sign)
log("\nSEND ")
log("%i" % sign)
watch="Plaintext="
data=""
while watch not in data:
dd = s.recv(BUFFER_SIZE)
log(dd)
data += dd
if "Authentication complete" not in data:
print "FAILED??"
verbose(data)
continue
plain=data[data.index(watch)+len(watch):].rstrip('\x00').rstrip('\x00\n')
plain="".join([chr((ord(x)) ^ (ord(y))) for (x,y) in zip(plain.decode('hex'), iv.decode('hex'))])
bmp.seek(ci-16,0)
bmp.write(plain)
decoded=True
s.close()
except ZeroDivisionError:
print "Error captured"
We let it run for a while and we can inspect the BMP from time to time to see how it progresses.
Then when interesting spots are identify we can restrict the random sampling to that region.
And soon:

Apparently I got lucky because the first area I revealed was the flag, while actually there were two other (useless) lines in the picture:

Challenge 4
128 May 14 19:35 ctxt4.txt 16975387 Jun 23 13:49 rom.png
First step
file rom.png rom.png: PNG image data, 30598 x 10240, 8-bit/color RGB, non-interlaced
That's a huge image!
To give an idea, here is a scaled-down version:
convert rom.png -resize 5% rom_scaled.png
And a zoom at scale 1:1 on the top left corner:
convert rom.png -crop 300x300-0-0 +repage rom_corner.png
It's apparently the photo of a chip die, a ROM by the filename and aspect and we can distinguish clear and dark spots, zeros and ones, or vice versa.
ROM dots are rectangles of 7x5 pixels, separators are 7px wide
Let's open the file in Gimp and crop borders on both sides, now we get a 30457x10240 grid, which lead to exact multiples:
30457/7 = 4351 10240/5 = 2048
Still in Gimp, let's resize it to 4351x2048 so one pixel per ROM dot and disable any interpolation!
We're left with two tones for the dots and a third for the separators.
Select the two tones of ROM dots and color them in black and white.
Save the result as rombw.png

And a zoom on the top left, scale 2:1

This simple technique worked because the ROM image was artificially created and was very regular.
For real ROM die pictures, see rompar by Adam Laurie.
In the last image we see the column structure:
8:8:1 8:8:1 ...
Fourth column shows something like a font table and the top half shows probably incremental values so given their pattern we guess we've to interpret those dots as 2-byte words, MSB, the left byte then the right byte, from top of the column to bottom of the column.
Adding one separator to the count to have as many separators as columns, we get (4351+1)/17 = 256 pairs of columns
Let's isolate the data by converting the image in PNM format, very convenient to manipulate.
So convenient that the only thing we've to do to convert to raw data is to convert to PBM (the black and white format) and cut the PBM header:
#!/bin/bash
pngtopnm rombw.png > rombw.pnm
for ((i=0;i<256;i++)); do
# Should we interpret black / white as 0/1 or 1/0 ?
pnmcut -left $(($i*17)) -width 16 rombw.pnm |ppmtopgm|pgmtopbm|pnminvert|dd bs=1 skip=11 >> rom.bin
# pnmcut -left $(($i*17)) -width 16 rombw.pnm |ppmtopgm|pgmtopbm|dd bs=1 skip=11 >> rom2.bin
done
rm rombw.pnm
file rom.bin rom.bin: Gameboy ROM: "4", [ROM+MBC1], ROM: 8Mbit, RAM: 64Kbit
Sounds like we got something!
I made rom.bin available here.
Running it in an emulator such as gngb shows a first message with the intermediate flag (here zoomed at 2:1):
So the intermediate flag is UGA-+pcnsgxp93
Second step
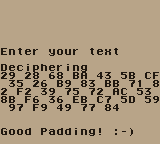
The it says "Enter your text" with a cursor that can move on an invisible 4x4 grid.
Pressing Enter (Gameboy Start):
Moving around and pressing X (Gameboy A) 64 times makes the "game" moving to the deciphering stage, where we see the text we entered, so the 4x4 grid is the 16 hexadecimal symbols.
Then:
It smells like padding oracle attack ;-)
All the difficulty will be to automate the attack.
It's also possible to enter only 32 symbols (16 bytes) and press Start but I didn't figure out if it can be useful for something or not.
Trying to launch the ROM in a more advanced tool such as no$gmb debugger fails and suggests VisualBoyAdvance:
I finally chose to drive directly gngb with xdotool and take screen snapshots with xwd, from x11-apps.
#!/bin/bash
DELAY=300
SLEEP1=2
SLEEP2=5
cc="${1}"
if [ ${#cc} != 64 ]; then
echo "Error ciphertext too short: $cc" >&2
exit 1
fi
gngb -a rom.bin &
dd() {
case $1 in
0) x2=0;y2=0;;
1) x2=1;y2=0;;
2) x2=2;y2=0;;
3) x2=3;y2=0;;
4) x2=0;y2=1;;
5) x2=1;y2=1;;
6) x2=2;y2=1;;
7) x2=3;y2=1;;
8) x2=0;y2=2;;
9) x2=1;y2=2;;
a) x2=2;y2=2;;
b) x2=3;y2=2;;
c) x2=0;y2=3;;
d) x2=1;y2=3;;
e) x2=2;y2=3;;
f) x2=3;y2=3;;
esac
while [ $x2 -gt $x ]; do s="${s} Right"; x=$(($x+1)); done
while [ $x2 -lt $x ]; do s="${s} Left"; x=$(($x-1)); done
while [ $y2 -gt $y ]; do s="${s} Down"; y=$(($y+1)); done
while [ $y2 -lt $y ]; do s="${s} Up"; y=$(($y-1)); done
s="${s} x"
}
x=0
y=0
sleep $SLEEP1
s="xdotool search Gngb key --delay $DELAY "
for i in $(echo $cc|sed 's/\(.\)/ \1/g'); do dd $i ;done
$s 2>/dev/null
sleep $SLEEP2
xwd -name Gngb|convert - png: > shot_${cc}.png
pkill gngb
Let's try the last block of ctxt4.txt where padding should be correct and the one before as IV:
./run-once.sh 292868ba435bcf3526b983bb7182f2397572ac538bf636ebc75d5997f9497784
But it's still awfully slow to type in the ciphertexts and it's just not doable without the --autoframeskip option of gngb.
In total it takes about 76s for one single run and we can't reduce the delay of keypresses below 300ms without missing key strokes.
So I patched gngb to run it faster (with --autoframeskip):
--- gngb-20060309/src/frame_skip.c 2015-06-26 09:01:51.867400703 +0200
+++ gngb-20060309/src/frame_skip.c 2015-06-26 09:01:51.867400703 +0200
@@ -100,7 +100,7 @@
if (conf.autoframeskip) {
if (rfd<target && f2skip==0 ) {
- while(get_ticks()<target) {
+ while(get_ticks()<target/25) { // faster!
if (conf.sleep_idle)
#ifdef HAVE_USLEEP
usleep(10);
So now I could take down the delay when pressing keys with xdotool to 20ms and the full run takes now 6.6s:
DELAY=20 SLEEP1=1 SLEEP2=1
Now the padding attack:
To check if the run went smoothly and led to a good or bad padding, we take a snapshot of the Gameboy screen at the end, crop it to keep the bottom, hash it and compare it with the known hashes of a good or a bad padding result.
The script is a bit ugly because I started in bash then moved to python for the tricky parts... CTF quality ;-)
#!/bin/bash
DELAY=20
SLEEP1=1
SLEEP2=1
KNOWN=""
pkill gngb
fast_patch/gngb-20060309/src/gngb -a rom.bin &
dd() {
case $1 in
0) x2=0;y2=0;;
1) x2=1;y2=0;;
2) x2=2;y2=0;;
3) x2=3;y2=0;;
4) x2=0;y2=1;;
5) x2=1;y2=1;;
6) x2=2;y2=1;;
7) x2=3;y2=1;;
8) x2=0;y2=2;;
9) x2=1;y2=2;;
a) x2=2;y2=2;;
b) x2=3;y2=2;;
c) x2=0;y2=3;;
d) x2=1;y2=3;;
e) x2=2;y2=3;;
f) x2=3;y2=3;;
esac
while [ $x2 -gt $x ]; do s="${s} Right"; x=$(($x+1)); done
while [ $x2 -lt $x ]; do s="${s} Left"; x=$(($x-1)); done
while [ $y2 -gt $y ]; do s="${s} Down"; y=$(($y+1)); done
while [ $y2 -lt $y ]; do s="${s} Up"; y=$(($y-1)); done
s="${s} x"
}
for ((n=$(((${#KNOWN}/2)+1));n<17;n++)); do
ccorig="292868ba435bcf3526b983bb7182f2397572ac538bf636ebc75d5997f9497784"
#ccorig="4ac2c9e5ac61834bda70725000435fa6292868ba435bcf3526b983bb7182f239"
#ccorig="023aed0485f26b3b066349bc7856adad4ac2c9e5ac61834bda70725000435fa6"
#ccorig="00000000000000000000000000000000023aed0485f26b3b066349bc7856adad"
# Trying all padding characters:
for ((bn=16;bn>0;bn--)); do
# Trying all printable characters:
#for ((bn=$((0x7E));bn>$((0x1F));bn--)); do
# or trying specific chars first
#for bc in " " ":" e t a i r o n s l h c d u p m g y f w b v k x j q z E T A I R O N S L H C D U P M G Y F W B V K X J Q Z 0 1 2 3 4 5 6 7 8 9; do
xdotool search Gngb key F11 2>/dev/null
x=0
y=0
sleep $SLEEP1
[ "$bn" != "" ] && bb=$(python -c "print '%02x' % (0x${ccorig:$(((16-$n)*2)):2}^$n^$bn)")
[ "$bc" != "" ] && bb=$(python -c "print '%02x' % (0x${ccorig:$(((16-$n)*2)):2}^$n^ord(\"$bc\"))")
cc=${ccorig:0:$(((16-n)*2))}
cc+=$bb
pad=$(python -c "print ('%02x' % $n)*$(($n-1))")
[ $n -gt 1 ] && cc+=$(python -c "print \"%0$((($n-1)*2))x\" % (0x${ccorig:$(((16-$n+1)*2)):$((($n-1)*2))}^0x${pad}^0x$KNOWN)")
cc+=${ccorig:32:32}
echo -n "$bn $bc $bb $cc"
s="xdotool search Gngb key --delay $DELAY "
for i in $(echo $cc|sed 's/\(.\)/ \1/g'); do dd $i ;done
$s 2>/dev/null
sleep $SLEEP2
# capture screen:
xwd -name Gngb|convert - pnm: > shot$cc.pnm
echo " done"
h="$(cat shot$cc.pnm|pnmcut -top 120 |md5sum|cut -d ' ' -f 1)"
if [ "$h" == 3b803e5a3e03d39288848a99f41a27b8 ]; then
# Didn't get the full input
echo Missed
[ "$bn" != "" ] && bn=$(($bn+1))
continue
fi
if [ "$h" == 4cad20f4a813ca01ee6709b7654dd8c0 ]; then
# Good padding
echo Good
echo $cc >> padding.log
touch shot$cc.flag
c=$(python -c "print chr(0x${ccorig:$(((16-$n)*2)):2}^$n^0x$bb)")
KNOWN=$(echo -n "$c"|xxd -p)$KNOWN
echo $KNOWN
echo $KNOWN|xxd -r -p|strings -n 1
break
fi
if [ "$h" == 505b8e70d3b80346a361132fb82161cf ]; then
# Bad padding
# At this point it may happen that we've enough input but
# some symbol was mistyped.
# We can check that last part of input was properly typed but
# we've up to 4 variants depending on the IV for each block
##h2="$(cat shot$cc.pnm|pnmcut -top 103 |md5sum|cut -d ' ' -f 1)"
##if [ "$h2" != 5a1dd1cb0823d108ac482890d129ba08 ] && \
## [ "$h2" != 0c6991bb943791f24774dd28974e1656 ] && \
## [ "$h2" != 5c82befbbfceb246c21ecad92e9a07fa ] && \
## [ "$h2" != 91dbd4d85b8216e70b1e3979bd78aab8 ]; then
## echo Missed
## [ "$bn" != "" ] && bn=$(($bn+1))
##fi
rm shot$cc.pnm
continue
fi
if [ "$h" != 505b8e70d3b80346a361132fb82161cf ]; then
# So far but not a bad padding? sth went wrong
echo Error
echo $cc >> padding.log
touch shot$cc.err
exit
fi
done
done
For the first run, we use the last two ciphertext blocks
ccorig="292868ba435bcf3526b983bb7182f2397572ac538bf636ebc75d5997f9497784"
We could just try all possible 256 values for each byte and let it run for hours, or do smarter hypotheses on the ciphertext.
Let's try to find the last byte of padding, should be between 0x01 and 0x0a (actually if it's 0x01 there is no other modification of the IV that could lead to a good padding):
for ((bn=16;bn>0;bn--)); do
This finds 0x05, so we can guess the padding is 0505050505
KNOWN="0505050505"
And from now on, only printable characters:
for ((bn=$((0x7E));bn>$((0x1F));bn--)); do
Or even a more restricted ordered set for faster findings (but this requires much more baby-sitting to adapt guesses accordingly to the findings)
for bc in " " ":" e t a i r o n s l h c d u p m g y f w b v k x j q z E T A I R O N S L H C D U P M G Y F W B V K X J Q Z 0 1 2 3 4 5 6 7 8 9; do
Next characters are "C", "o", "n", "g".
We're supposed to discover the plaintext backwards but it seems it has been forged backwards to discover it in a more natural order. So we can guess the first word is "Congratulations".
Let's test this hypothesis and find the first char of that block:
KNOWN=$(echo -n "alutargnoC"|xxd -p)"0505050505"
for bc in t; do
Good padding! This means we successfully revealed the last block:
talutargnoC\x05\x05\x05\x05\x05
Next one:
KNOWN=$(echo -n "noi"|xxd -p)
ccorig="4ac2c9e5ac61834bda70725000435fa6292868ba435bcf3526b983bb7182f239"
for bc in " " ":" e t a i r o n s ...
And so forth. Each time trying to guess parts of the plaintext, narrowing or widening the charset to explore to accelerate the padding attack.
Omitting the padding and writing the plaintext backwards, it gives:
Congratulations! The final flag for Step4 is Ozn"9269dC&d75
Second step, "fox" version
For the automation phase, @foxTN instrumented VisualBoyAdvance, the emulator suggested by the ROM.
Here is his version:
The problem now is to find a way to automate the ciphertext insertion, trigger a decryption and get the output from the game.
After some reverse engineering of the ROM I collected the following information:
- The ciphertext buffer is on the stack at 0xdcdb
- The length of the inserted ciphertext is at 0xdbde. The ROM constantly checks this value, if it's >= 0x20 a decryption starts
- At 0x9a00 (video memory) we can get the output (good or bad padding)
So I hooked reads and writes from memory by patching the emulator and get some kind of instrumentation. The file we need to modify is "src/gb/GB.cpp", in particular the functions "gbWriteMemory" and "gbReadMemory".
For points 1 and 2 I added this code to the beginning of "gbReadMemory" (it's really bad code, but I was in a hurry):
FILE* f;
u8 buf[0x100];
if (address == 0xdbde) {
f = fopen("/tmp/start_decryption", "r");
if (f != NULL) {
fclose(f);
remove("/tmp/start_decryption");
gbMemoryMap[address>>12][address&0x0fff] = 0x20;
}
}
if (address >= 0xdcdb && address < (0xdcdb+0x20)) {
f = fopen("/tmp/ciphertext", "r");
if (f != NULL) {
fread(buf, 1, 0x20, f);
fclose(f);
return buf[address - 0xdcdb];
}
}
For point 3 I added this to the beginning of "gbWriteMemory":
if (address >= 0x9a00 && address <= 0x9a0f) {
FILE* f = fopen("/tmp/output", "w");
for (int i=0; i<16; i++) {
fputc(gbMemoryMap[(0x9a00+i)>>12][(0x9a00+i)&0x0fff], f);
}
fclose(f);
}
This basically allows us to do the following:
- Instead of reading from the actual buffer the emulator will read the ciphertext from /tmp/ciphertext
- By creating the file /tmp/start_decryption we will trigger a decryption
- We will get the output of the decryption in /tmp/output
The only part we miss is to press "start" (i.e.: the Enter key) to get back the screen to insert a new ciphertext. For this I faked the pressing of Enter using Python.
The final exploit is the following:
from paddingoracle import BadPaddingException, PaddingOracle
from pykeyboard import PyKeyboard
from base64 import b64encode, b64decode
from urllib import quote, unquote
import requests
import socket
import time
import os
class PadBuster(PaddingOracle):
def __init__(self, **kwargs):
self.k = PyKeyboard()
super(PadBuster, self).__init__(**kwargs)
def press(self, key, n=1, interval=0):
for _ in range(n):
self.k.press_key(key)
time.sleep(0.01)
self.k.release_key(key)
print "Pressed Key =", key
time.sleep(interval)
def oracle(self, data, **kwargs):
while True:
with open("/tmp/ciphertext", "w") as cipher:
cipher.write(data)
# trigger decryption
with open("/tmp/start_decryption", "w") as cipher:
cipher.write(data)
# wait for decryption being done
print "Waiting for decryption..."
time.sleep(0.5)
print "Reading output..."
# check output
try:
with open("/tmp/output") as out:
result = out.read()
os.remove("/tmp/output")
print "RESULT =", result
except:
print "Reading output failed..."
result = ""
# press enter
self.press(self.k.enter_key)
time.sleep(0.5)
if "Good" in result:
logging.debug('No padding exception raised on %r', data)
return
elif "Bad" in result:
raise BadPaddingException
else:
print "FAILURE!!!"
print "Press enter to continue"
raw_input()
print "Retrying in 10s"
time.sleep(10)
if __name__ == '__main__':
import logging
import sys
if not sys.argv[1:]:
print 'Usage: %s <ciphertext>' % (sys.argv[0], )
sys.exit(1)
logging.basicConfig(level=logging.DEBUG)
print "Starting in 5sec"
time.sleep(5)
encrypted = sys.argv[1].decode('hex')
padbuster = PadBuster()
cookie = padbuster.decrypt(encrypted, block_size=16, iv=bytearray(16))
print('Decrypted: %s => %r' % (sys.argv[1], cookie))
To speed things up we can pass the option "-T 1000" to VBA to make it run 10 times faster than normal. I had some issues with the emulator going into some kind of deadlock from time to time. I don't know why that was happening but I added some code to the exploit to handle failures and recover.
Second step revisited
Due to the very large ROM size and the nature of the challenge, I suspect there is some white-box cryptography in there.
Let's analyze the ROM.
Two useful documents to understand a Gameboy CPU and ROM:
- unofficial Game Boy CPU Manual (pdf)
- Game Boy opcodes
The ROM cartridge is not entirely directly accessible, only the first bank of 0x4000 bytes (16kB), then other banks are mapped between 0x4000 and 0x8000. How this mapping is done depends on the cartridge memory controller.
Some bytes at the beginning of the ROM give us some info:
- 0x134-0x142: title="4"
- 0x143=0x00: not col or gb(?)
- 0x146=0x00: gb functions
- 0x147=0x01: cartridge type: ROM+MBC1
- 0x148=0x05: ROM size = 8Mbits = 1 MB = 64 banks
- 0x149=0x02: RAM = 64kbits = 8kB = 1 bank
So it's using Memory Bank Controller 1:
The MBC1 defaults to 16Mbit ROM/8KByte RAM mode on power up.
Writing a value (XXXXXXXS - X = Don't care, S = Memory model select) into 6000-7FFF area will select the memory model to use. S = 0 selects 16/8 mode. S = 1 selects 4/32 mode.
I didn't observe any writing in that area.
Writing a value (XXXBBBBB - X = Don't cares, B = bank select bits) into 2000-3FFF area will select an appropriate ROM bank at 4000-7FFF. Values of 0 and 1 do the same thing and point to ROM bank 1. Rom bank 0 is not accessible from 4000-7FFF and can only be read from 0000-3FFF.
Writing a value (XXXXXXBB - X = Don't care, B = bank select bits) into 4000-5FFF area will set the two most significant ROM address lines.
I didn't observe any writing in that area.
I'm anticipating a bit but I observed memory reads and writes during emulation and there were only writes "on ROM" in the area 0x2000-0x3FFF, even some with value 0x22 (bank 34) while MBC1 description suggests that bank 34 should be accessed by writing 0x02 in 0x2000-0x3FFF and 0x01 in 0x4000-0x5FFF and writing 0x22 would be the same as writing 0x02.
I like to reverse things visually so let's trace all memory accesses by patching again gngb.
Actually every single instruction is preceded by an explicit memory read as fetch in the emulator, so we want to filter those reads out by patching again gngb.
diff --git a/src/cpu.c b/src/cpu.c
index f03a811..1227fa4 100644
--- a/src/cpu.c
+++ b/src/cpu.c
@@ -30,6 +30,7 @@ GB_CPU *gbcpu=0;
//extern Sint32 gdma_cycle;
+Uint8 myflag_fetch=0;
static Uint8 t8;
static Sint8 st8;
static Uint16 t16;
@@ -183,7 +184,10 @@ __inline__ Uint8 gbcpu_exec_one(void)
gbcpu->int_flag=1;
gbcpu->ei_flag=0;
}
+ myflag_fetch=1;
mem_read_fast(PC,opcode);
+ myflag_fetch=0;
+ printf("I%c%c%c", gbcpu->pc.b.h, gbcpu->pc.b.l, opcode);
PC++;
switch(opcode) {
diff --git a/src/memory.h b/src/memory.h
index 995da0a..3f8a75f 100644
--- a/src/memory.h
+++ b/src/memory.h
@@ -23,6 +23,7 @@
#include "global.h"
#include <SDL.h>
+extern Uint8 myflag_fetch;
/* mbc1 mem mode type */
#define MBC1_16_8_MEM_MODE 0
@@ -156,14 +157,17 @@ void mem_write_ff(Uint16 adr,Uint8 v);
/* To use this macro you don't have to use autoincrementation in argument */
#define mem_read_fast(a,v) {\
+ if (!myflag_fetch) printf("R%c%c", a >> 8, a & 0xff);\
if (mem_read_tab[((a)>>12)&0xff].type!=MEM_DIRECT_ACCESS) {\
(v)=mem_read_tab[((a)>>12)&0xff].f((a));\
} else {\
(v)=mem_read_tab[((a)>>12)&0xff].b[(a)&0xfff];\
}\
+ if (!myflag_fetch) printf("%c", v);\
}
#define mem_write_fast(a,v) {\
+ printf("W%c%c%c", a >> 8, a & 0xff, v);\
if (mem_write_tab[((a)>>12)&0xff].type!=MEM_DIRECT_ACCESS) {\
mem_write_tab[((a)>>12)&0xff].f((a),(v));\
} else {\
Because tracing is slightly slowing down gngb, it's good to make the xdotool delay slightly longer:
DELAY=30
General memory map:
Interrupt Enable Register --------------------------- FFFF Internal RAM --------------------------- FF80 Empty but unusable for I/O --------------------------- FF4C I/O ports --------------------------- FF00 Empty but unusable for I/O --------------------------- FEA0 Sprite Attrib Memory (OAM) --------------------------- FE00 Echo of 8kB Internal RAM --------------------------- E000 8kB Internal RAM --------------------------- C000 8kB switchable RAM bank --------------------------- A000 8kB Video RAM --------------------------- 8000 16kB switchable ROM bank --------------------------- 4000 16kB ROM bank #0 --------------------------- 0000
By default gngb outputs some info on the console, you can clean them from the log or comment the corresponding printf() in src/rom.c
Then I traced one single execution with the last two ciphertext blocks.
The trace has 68M instructions, 31M reads and 1.6M writes.
The lengthy part is when the ciphertext is typed in.
We observe five similar patterns that look like a white-box execution with all those "random" reads from a large memory area.
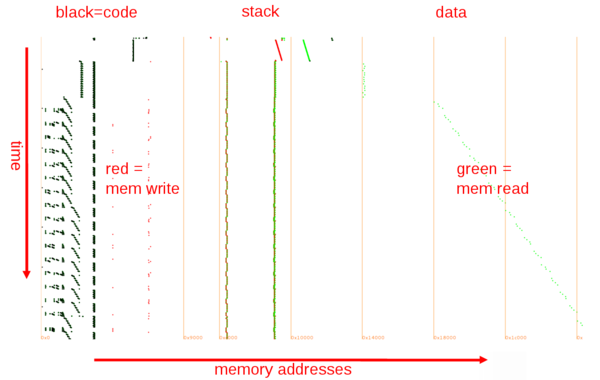
Instructions in black, reads in green and writes in red, X axis is memory addresses and Y axis is time axis, starting on top and going down:
Let's filter the trace to the bottom part (from when instruction address == 0x5041 to when addr == 0x5395).
It's not visible at this scale but there are also annoying regular interrupt handlers that we can filter out too: from when addr == 0x0040 to when addr == 0x007d.
Remember that it's not the ROM but the memory as seen by the CPU, where all ROM banks (except the first one) are mapped successively in 0x4000-0x7fff.
So let's interpret all writes to 0x2000-0x3fff and remap 0x4000-0x7fff at 0x100000 (so e.g. something visible at 0x23456 is actually from ROM address 0x13456).
In each of the four white-box executions we see nine bumps, corresponding to the nine MixColumns of a 10-round AES-128.
Further analysis and zooms on the graph show functionality of that part of the trace:
- white-box #2: processes one fixed block (5FEEB70AE1C37984A46EFBC9F523EA32) and outputs E8CBF8217D54F8042272F8395E235621
- This sequence is used to XOR a range of ROM 0x57c-0x82b (minus some bytes) and decode it in RAM at 0xd000-0xd2b9. This will become some executable code after some more manipulation of some of its bytes... That code will be used after the third white-box to check the padding.
- white-box #3: the one processing the input ciphertext (the second block, as the first one is the IV, so here: 7572ac538bf636ebc75d5997f9497784). The plaintext, still, is not directly observable, even p^iv is not.
- then comes some processing from the decoded instructions to check the padding. We'll come back on that one later.
- white-box #4: depending on the padding check, it'll decipher f24e78e4b9c0e075fba1b518e065b146 into "Good Padding! :-" or another block if bad padding.
- white-box #5: idem, the second part of the result message, here 3bcc1cc8f9a44d9c09ae48064fb73e2f producing ")\n\x00..."
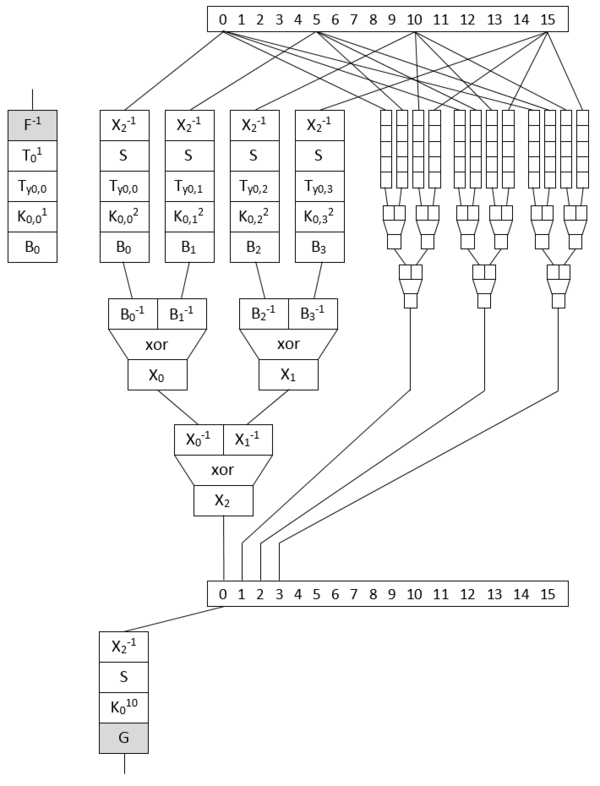
Now we've to figure out the structure and location of the white-box tables.
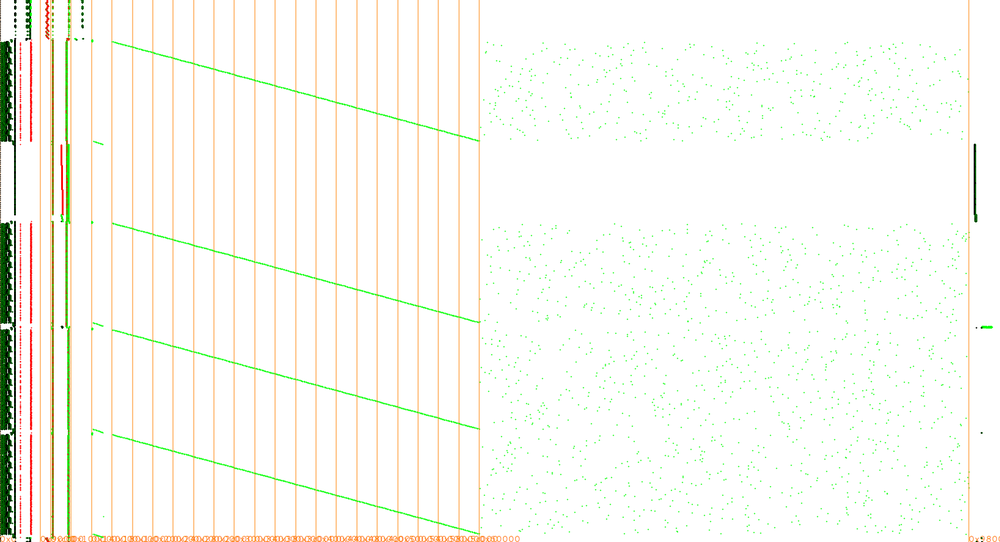
Let's zoom on the stack of one white-box.
It starts with
with some "random" accesses to a small table of 256 bytes around 0x04000.
Actually for each input byte x it reads at 0x04008+x so 0x04008:0x04107 is our first white-box table T1 and the accesses we observe are to transpose the AES input (green) into its internal state (red) and apply T1() on each byte, typically to apply the input encoding.
So if input bytes are stored as 0,1,2,3,4,5,6,7,8,9,a,b,c,d,e,f the AES state is represented as a grid:
0 4 8 c 1 5 9 d 2 6 a e 3 7 b f
and stored in memory row by row as 0,4,8,c,1,5,9,d,2,6,a,e,3,7,b,f.
Then nine rounds with for each this type of pattern:
Again the read (green) and write (red) patterns show the structure:
- cells 0,1,2,3 are written from 0,5,a,f
- cells 4,5,6,7 are written from 4,9,e,3
- cells 8,9,a,b are written from 8,d,2,7
- cells c,d,e,f are written from c,1,6,b
They come together with 64 "random" reads from 64*9 successive 256-byte tables and 48 reads from 3 very large 65536-byte tables that can be observed when zooming out on the whole memory:
Observing the actual values show that to compute cell 0, assume w,x,y,z are read from cells 0,5,a,f, then they are replaced at round N by w'=T_roundN_byte0_0(w), x'=T_roundN_byte0_1(x), y'=T_roundN_byte0_2(y), z'=T_roundN_byte0_3(z), then wx=Tlarge1(w', x') and yz=Tlarge2(y', z') and finally cell0=Tlarge3(wx, yx):
Then the final round:
Besides the table substitution, the reordering of the state is interesting:
0 4 8 c 048c 159d 26ae 37bf 1 5 9 d 2 6 a e 3 7 b f
becomes
0 5 a f 05af 49e3 8d27 c16b 4 9 e 3 8 d 2 7 c 1 6 b
This reordering can only be explained by a ShiftRows and a transposition to restore the natural order of the output.
Note that I didn't say the inversed ShiftRow, so actually just by looking at those dots we can affirm that it's very probably an AES-128 encryption!!, and not a decryption as we could have expected.
Similarly the intermediate rounds are reordering the internal state
0 4 8 c 1 5 9 d 2 6 a e 3 7 b f
as
f(0,5,a,f) f(4,9,e,3) f(8,d,2,7) f(c,1,6,b) f(0,5,a,f) f(4,9,e,3) f(8,d,2,7) f(c,1,6,b) f(0,5,a,f) f(4,9,e,3) f(8,d,2,7) f(c,1,6,b) f(0,5,a,f) f(4,9,e,3) f(8,d,2,7) f(c,1,6,b)
which is explained by the application of a ShiftRows and a MixColumns
This structure is not the one of Chow or derivatives but we've seen it before, in the NoSuchCon 2013 challenge:
Eloi Vanderbéken, author of the NSC challenge, published his generator so let's try to extract our tables and reuse some of the NSC code.
When extracting tables, it's always good to verify them by checking their statistical distribution and this was useful to see there was a little quirk in the large XOR tables: tables are split in ROM banks where first two bytes were always 0x02 0x40 so the table started with an offset of 2 bytes, but last 14 bytes were some 0xff so for every bank, there is 16 bytes missing. One read access in the last white-box shows that when it needs to access one of those 16 bytes, it reads it from another table of 192 bytes (for 12 banks) from 0x5208 to 0x52c7. To find the exact positions, I made the stats on the tables of each bank, short by 16 bytes, and looked for those 16 missing values in a consecutive chunk of memory around 0x5200.
While knowing the external encodings is not required to break the white-box, as we'll see in a moment, it would be nice to recover the output external encoding table as well to get a functional white-box. For that one, it's important to come back on the code checking the plaintext padding because the other white-boxes don't use any external encoding table to recover the output! What you see in plain such as the "Good Padding! :-" seen earlier is still technically encoded with external encodings, it was just constructed as such so those white-boxes are not a strict equivalent of a plain AES.
This padding checking code was decoded earlier, remember? and it's quite convoluted. The reason is that if the AES plaintext was made more accessible, it would have been easy to spot it in the trace (e.g. by data correlation over a few traces) and to observe directly the flag present in the first block (to be xored with a null IV, so in plain).
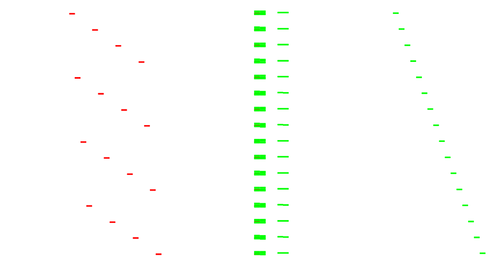
Here is a zoom on the instructions and stack:
The processed block is the last one of the challenge ciphertext, with a padding 0505050505.
We see some effort was made to run in constant time: it always run 16 times, with one a bit different (the fifth).
A first loop identifies the value of the last padding byte, here 0x05.
Then five loops test successively the last five bytes (including the one read just before!)
So to get the value of the padding bytes, the external encoding table was used, right?
Actually not.
To "decode" one padding byte, it takes the corresponding IV byte, it makes a guess on the padding value (between 1 and 16) and read the corresponding externally encoded value in one of 16 tables then compares it with the white-box output.
So e.g. for the last byte, IV=0x39 and the 16 tests in the loop are:
G(0x39^0x01)=0x30 != white-box output=0x2c ... G(0x39^0x05)=0x2c == white-box output=0x2c ...
We don't have directly the table to revert the external encoding but we've 16 related tables. So by taking e.g. the first one, taking care of the xor 0x01 and inverting it we can forge the missing table.
Here is my current understanding of the ROM map:
0x00000:0x000ff vector table 0x00100-0x00103 entry point: NOP, JP 0x150 0x00104-0x0014f internal ROM information 0x00150:0x03bd2 second entry point, some code 0x0215a:0x023f1 some code for padding checking that is decoded (xor) after second white-box 0x04000 08 40 08 41 08 42 08 52 0x04008:0x04107 init_invsub 0x04108:0x05207 finalTable 0x05208:0x052c7 xorTables 12*16 missing parts 0x08000 02 40 0x08002:0x0a001 roundTable1.0 0x0c000 02 40 0x0c002:0x0e001 roundTable1.1 ... 0x48000 02 40 0x48002:0x4a001 roundTable9.0 0x4c000 02 40 0x4c002:0x4e001 roundTable9.1 0x50000 02 40 0x50002:0x53FF1 \ ... xorTables (last 16 bytes missing: chunks of 0x3ff8 instead of 0x4000) 0x7c002:0x7FFF1 / 0x88000:... some code 0x893a6:0x8a3a5 16 G(iv^pad) tables 0x8a3a6 A8 63 00 11 22 33 44 55 66 77 88 99 AA BB CC DD EE FF
We've now everything to extract all tables and write them in a file compatible with the NSC2013 white-box code:
#!/usr/bin/env python
# pad=1..16 whatever
pad=1
def validate(t):
stats=[0]*256
for x in t:
stats[ord(x)]+=1
# all elements must appear the same nr of times
assert stats.count(stats[0]) == len(stats)
def inv(t):
tinv=[0]*256
for i in range(len(t)):
tinv[ord(t[i])]=chr(i)
return ''.join(tinv)
rom = open('rom.bin', 'rb').read()
with open('wbt_rom', 'wb') as wbt:
init_invsub = rom[0x4008:0x4008+0x100]
validate(init_invsub)
init_sub = inv(init_invsub)
validate(init_sub)
wbt.write(init_sub)
wbt.write(init_invsub)
final_IV1 = rom[0x892a6+(0x100*pad):0x892a6+(0x100*pad)+0x100]
final_sub = ''. join([final_IV1[i^pad] for i in range(256)])
validate(final_sub)
wbt.write(final_sub)
final_invsub = inv(final_sub)
validate(final_invsub)
wbt.write(final_invsub)
xorTable1=""
for i in range(0x10000/0x4000):
xorTable1+=rom[0x50002+(i*0x4000):0x50002+(i*0x4000)+0x3ff0]
xorTable1+=rom[0x5208+(i*16):0x5208+(i*16)+16]
validate(xorTable1)
xorTable2=""
for i in range(0x10000/0x4000):
xorTable2+=rom[0x60002+(i*0x4000):0x60002+(i*0x4000)+0x3ff0]
xorTable2+=rom[0x5248+(i*16):0x5248+(i*16)+16]
validate(xorTable2)
xorTable3=""
for i in range(0x10000/0x4000):
xorTable3+=rom[0x70002+(i*0x4000):0x70002+(i*0x4000)+0x3ff0]
xorTable3+=rom[0x5288+(i*16):0x5288+(i*16)+16]
validate(xorTable3)
wbt.write(xorTable1)
wbt.write(xorTable2)
wbt.write(xorTable3)
for i in range(9):
roundTable=rom[0x8002+0x8000*i:0x8002+0x8000*i+0x2000]+rom[0x8002+0x8000*i+0x4000:0x8002+0x8000*i+0x4000+0x2000]
validate(roundTable)
wbt.write(roundTable)
finalTable = rom[0x4208:0x4208+(0x100*16)]
validate(finalTable)
wbt.write(finalTable)
The resulting file is to be used with some white-box code derived directly from Eloi's generator.
#include <stdio.h>
#include <stdlib.h>
#include <stdint.h>
typedef struct sub_s {
uint8_t sub[0x100];
uint8_t inv_sub[0x100];
} *sub_t;
typedef struct aes_wb_s {
struct sub_s initSub;
struct sub_s finalSub;
uint8_t xorTables[3][0x10000];
uint8_t roundTables[9][16][4][0x100];
uint8_t finalTable[16][0x100];
} *aes_wb_t;
unsigned char is_hex_char(char c)
{
return (
(c >= '0' && c <= '9') ||
(c >= 'a' && c <= 'f') ||
(c >= 'A' && c <= 'F')
);
}
int main(int argc, char *argv[])
{
struct aes_wb_s aes;
uint8_t i, round;
uint8_t t[12][16];
uint8_t m[16];
for(i = 0; i < 32; i += 2)
{
if(is_hex_char(argv[1][i]) == 0 || is_hex_char(argv[1][i + 1]) == 0)
return EXIT_FAILURE;
unsigned char str_bytes[3] = {
argv[1][i],
argv[1][i + 1],
0
};
m[ i / 2] = strtoul((const char*)str_bytes, NULL, 16);
}
FILE* f;
f = fopen("wbt_rom", "rb");
fread(&aes, 1, sizeof(aes), f);
fclose(f);
printf("Input: ");
for (i = 0; i < 16; i++)
printf("%02X ", m[i]);
printf("\n");
for (i = 0; i < 16; i++)
t[0][(i%4u)*4 + (i/4u)] = aes.initSub.inv_sub[m[i]];
printf("Enc in: ");
for (i = 0; i < 16; i++)
printf("%02X ", t[0][i]);
printf("\n");
for (round = 1; round < 10; round ++)
{
for (i = 0; i < 16; i++)
{
uint8_t b[4];
uint8_t j;
for (j = 0; j < 4; j++) {
b[j] = aes.roundTables[round-1][i][j][t[round-1][j*4+((i+j)%4u)]];
}
t[round][i] = aes.xorTables[2][(aes.xorTables[0][(b[0]<<8)|b[1]] << 8) | aes.xorTables[1][(b[2]<<8)|b[3]]];
}
}
for (i = 0; i < 16; i++)
t[10][i/4u + (i%4u)*4] = aes.finalTable[i][t[9][(i&(~3)) +((i+i/4)%4u)]];
printf("Enc out: ");
for (i = 0; i < 16; i++)
printf("%02X ", t[10][i]);
printf("\n");
printf("Output: ");
for (i = 0; i < 16; i++)
printf("%02X ", aes.finalSub.inv_sub[t[10][i]]);
printf("\n");
return 0;
}
Let's try on our last ciphertext block:
./nosuchcon_2013_whitebox 7572ac538bf636ebc75d5997f9497784 Input: 75 72 AC 53 8B F6 36 EB C7 5D 59 97 F9 49 77 84 Enc in: A3 5C 58 89 6A 90 D9 3F 6F 4F 2F 51 37 3A BC 16 Enc out: A7 C7 58 98 72 74 59 F9 0D F7 89 E3 B0 7A D0 2C Output: 5D 49 04 CF 37 3A BD 52 48 D6 C0 BE 74 87 F7 3C
XORing the output with the previous block as IV:
"%x" % (0x5D4904CF373ABD5248D6C0BE7487F73C ^0x292868ba435bcf3526b983bb7182f239)
=> '74616c75746172676e6f430505050505'
which is indeed the 'talutargnoC' followed by the padding.
Last white-box, the one outputting ")\n" :
./nosuchcon_2013_whitebox 3bcc1cc8f9a44d9c09ae48064fb73e2f Input: 3B CC 1C C8 F9 A4 4D 9C 09 AE 48 06 4F B7 3E 2F Enc in: B4 89 83 1E 84 6D A0 DF 92 7E 98 C3 C1 5B 59 4C Enc out: 29 0A 00 00 00 00 00 00 00 00 00 00 00 00 00 00 Output: C4 90 72 72 72 72 72 72 72 72 72 72 72 72 72 72
Useful output is, as said earlier, the encoded output.
So we've a working code-lifting, err I mean table-lifting, of the white-box \o/
Second step revisited, again
But we didn't have to go that far and reverse the external encodings because only with the inner rounds and xor tables, we can break the key, as explained in our NoSuchCon 2013 challenge write-up because the internal encoding X2 is reused between rounds (normal, it's already very large).
Running the attack on the white-box file with the code from my NSC write-up reveals immediately the key (here attacking round 3, could be any between 2 and 9):
./nosuchcon_2013_whitebox_rom_break R3K candidate: F886846C0E10C0A3867562504BC9BF60 K00: 4A7BB85DC1446AA1112222223B2A99FF K01: AE95AEBF6FD1C41E7EF3E63C45D97FC3 K02: 994780D1F69644CF8865A2F3CDBCDD30 K03: F886846C0E10C0A3867562504BC9BF60 K04: 2D8E54DF239E947CA5EBF62CEE22494C K05: AEB57DF78D2BE98B28C01FA7C6E256EB K06: 160494439B2F7DC8B3EF626F750D3484 K07: 811CCBDE1A33B616A9DCD479DCD1E0FD K08: 3FFD9F5825CE294E8C12FD3750C31DCA K09: 0A59EB0B2F97C245A3853F72F34622B8 K10: 66CA8706495D4543EAD87A31199E5889 aes.xorTables[2] mapping: 00:7B 01:02 02:DA 03:5C 04:2C 05:70 06:F0 07:E9 08:D6 09:3D 0A:F3 0B:42 0C:F2 0D:ED 0E:A3 0F:79 10:A7 11:67 12:9D 13:07 14:EC 15:43 16:23 17:6D 18:11 19:4E 1A:10 1B:3B 1C:CA 1D:A4 1E:74 1F:F8 20:E3 21:EE 22:8F 23:9C 24:38 25:1B 26:AF 27:D1 28:6E 29:06 2A:1C 2B:A0 2C:4B 2D:AE 2E:68 2F:9F 30:6A 31:C8 32:E4 33:5E 34:E0 35:A8 36:05 37:F6 38:30 39:69 3A:57 3B:9E 3C:51 3D:B8 3E:D9 3F:62 40:5D 41:E1 42:56 43:36 44:FB 45:5B 46:C3 47:AC 48:BE 49:93 4A:7E 4B:27 4C:59 4D:A2 4E:BA 4F:91 50:AD 51:C1 52:EA 53:92 54:7C 55:76 56:29 57:4D 58:EB 59:71 5A:54 5B:D3 5C:13 5D:28 5E:35 5F:12 60:D2 61:20 62:F1 63:2F 64:3E 65:E7 66:CB 67:9A 68:DB 69:61 6A:C6 6B:3A 6C:DE 6D:FD 6E:1A 6F:B9 70:2B 71:F4 72:00 73:2A 74:8E 75:17 76:D8 77:96 78:80 79:99 7A:83 7B:15 7C:33 7D:84 7E:08 7F:52 80:CF 81:7F 82:BB 83:E2 84:1F 85:1E 86:89 87:01 88:0B 89:0C 8A:90 8B:0D 8C:98 8D:E5 8E:14 8F:94 90:53 91:25 92:DD 93:CE 94:3C 95:D5 96:87 97:16 98:0F 99:24 9A:95 9B:1D 9C:22 9D:E8 9E:77 9F:40 A0:DF A1:C0 A2:82 A3:19 A4:50 A5:8D A6:65 A7:49 A8:9B A9:D7 AA:B1 AB:63 AC:81 AD:34 AE:73 AF:78 B0:BF B1:37 B2:60 B3:3F B4:64 B5:32 B6:8C B7:44 B8:09 B9:86 BA:FF BB:75 BC:FE BD:D4 BE:A5 BF:45 C0:C4 C1:C9 C2:C5 C3:BC C4:CD C5:EF C6:66 C7:0A C8:4F C9:0E CA:5F CB:A9 CC:6C CD:2E CE:B3 CF:F5 D0:47 D1:48 D2:21 D3:FC D4:55 D5:D0 D6:46 D7:E6 D8:97 D9:04 DA:72 DB:5A DC:FA DD:C7 DE:DC DF:58 E0:AB E1:A6 E2:A1 E3:F7 E4:6B E5:B6 E6:26 E7:8A E8:CC E9:C2 EA:03 EB:85 EC:B5 ED:B2 EE:39 EF:41 F0:B4 F1:F9 F2:AA F3:18 F4:7D F5:88 F6:6F F7:31 F8:4C F9:B7 FA:7A FB:B0 FC:BD FD:4A FE:8B FF:2D
So the AES-128 key is 4A7BB85DC1446AA1112222223B2A99FF!
This attack took 1.8s on my laptop.
Let's try it on the last ciphertext block (taken as AES plaintext...):
echo "7572ac538bf636ebc75d5997f9497784"|xxd -r -p|openssl enc -aes-128-ecb -nopad -K 4A7BB85DC1446AA1112222223B2A99FF|xxd -p
5d4904cf373abd5248d6c0be7487f73c
"%x" % (0x5D4904CF373ABD5248D6C0BE7487F73C ^0x292868ba435bcf3526b983bb7182f239)
=> '74616c75746172676e6f430505050505'
Note that we can't decrypt the challenge file in one single call to openssl because what we have is a mix of a CBC decryption mode with an AES encryption...
Second step revisited, the sequel
Compared to NoSuchCon 2013, here we have recovered the external encodings (even if they made some effort to not include directly such a table to check the padding) therefore there is another attack possible on the finalTable with the knowledge of the output external encoding table:
- For the first finalTable, choose arbitrarily a (externally encoded) output byte value
- Make a guess for the corresponding round key byte
- Propagate output byte till getting the corresponding clear input byte (via reverse G, then xor with kR10[0], then reverse Sbox) and encoded input byte (via reverse finalTable), this gives us one correspondence of X2 table.
- We know substitution tables are the same for all bytes of the state so let's use the same input and so the same X2 entry for the next finalTable table. It determines uniquely the value before xor with the kR10[1] (via X2_inv, then Sbox) and the value after (via finalTable, then reverse G) therefore the value of that key byte
- Go on for all kR10 key bytes. So per kR10[0] key byte guess this gives one single full 16-byte kR10 key.
- Try other guesses for the initial kR10[0] key byte
- At the end we have 256 possible kR10 keys -> roll back the AES key scheduling to get the 256 corresponding AES keys and bruteforce them with one plaintext/ciphertext pair.
If one wants to reverse completely X2, he can run the attack with all different values for the externally encoded output byte. Here we computed only one entry of the X2 table.
#!/usr/bin/env python
from Crypto.Cipher import AES
rom=open('wbt_rom', 'rb').read()
Ginv=[ord(x) for x in rom[3*256:4*256]]
rom=rom[4*256 + 3*256*256 + 9*16*4*256:]
finalTable=[]
for i in range(0,16*256,256):
finalTable.append([ord(x) for x in rom[i:i+256]])
pref="3BCC1CC8F9A44D9C09AE48064FB73E2F".decode('hex')
cpref="290A0000000000000000000000000000".decode('hex')
cref=''.join([chr(Ginv[ord(x)]) for x in cpref])
finalTable_inv=range(16)
for b in range(16):
finalTable_inv[b]=range(256)
for i in range(256):
finalTable_inv[b][finalTable[b][i]]=i
Sbox=\
[0x63,0x7C,0x77,0x7B,0xF2,0x6B,0x6F,0xC5,0x30,0x01,0x67,0x2B,0xFE,0xD7,0xAB,0x76,
0xCA,0x82,0xC9,0x7D,0xFA,0x59,0x47,0xF0,0xAD,0xD4,0xA2,0xAF,0x9C,0xA4,0x72,0xC0,
0xB7,0xFD,0x93,0x26,0x36,0x3F,0xF7,0xCC,0x34,0xA5,0xE5,0xF1,0x71,0xD8,0x31,0x15,
0x04,0xC7,0x23,0xC3,0x18,0x96,0x05,0x9A,0x07,0x12,0x80,0xE2,0xEB,0x27,0xB2,0x75,
0x09,0x83,0x2C,0x1A,0x1B,0x6E,0x5A,0xA0,0x52,0x3B,0xD6,0xB3,0x29,0xE3,0x2F,0x84,
0x53,0xD1,0x00,0xED,0x20,0xFC,0xB1,0x5B,0x6A,0xCB,0xBE,0x39,0x4A,0x4C,0x58,0xCF,
0xD0,0xEF,0xAA,0xFB,0x43,0x4D,0x33,0x85,0x45,0xF9,0x02,0x7F,0x50,0x3C,0x9F,0xA8,
0x51,0xA3,0x40,0x8F,0x92,0x9D,0x38,0xF5,0xBC,0xB6,0xDA,0x21,0x10,0xFF,0xF3,0xD2,
0xCD,0x0C,0x13,0xEC,0x5F,0x97,0x44,0x17,0xC4,0xA7,0x7E,0x3D,0x64,0x5D,0x19,0x73,
0x60,0x81,0x4F,0xDC,0x22,0x2A,0x90,0x88,0x46,0xEE,0xB8,0x14,0xDE,0x5E,0x0B,0xDB,
0xE0,0x32,0x3A,0x0A,0x49,0x06,0x24,0x5C,0xC2,0xD3,0xAC,0x62,0x91,0x95,0xE4,0x79,
0xE7,0xC8,0x37,0x6D,0x8D,0xD5,0x4E,0xA9,0x6C,0x56,0xF4,0xEA,0x65,0x7A,0xAE,0x08,
0xBA,0x78,0x25,0x2E,0x1C,0xA6,0xB4,0xC6,0xE8,0xDD,0x74,0x1F,0x4B,0xBD,0x8B,0x8A,
0x70,0x3E,0xB5,0x66,0x48,0x03,0xF6,0x0E,0x61,0x35,0x57,0xB9,0x86,0xC1,0x1D,0x9E,
0xE1,0xF8,0x98,0x11,0x69,0xD9,0x8E,0x94,0x9B,0x1E,0x87,0xE9,0xCE,0x55,0x28,0xDF,
0x8C,0xA1,0x89,0x0D,0xBF,0xE6,0x42,0x68,0x41,0x99,0x2D,0x0F,0xB0,0x54,0xBB,0x16]
Sbox_inv=[0x00] * 256
for i in range(256):
Sbox_inv[Sbox[i]]=i
e_ctxt=[-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1]
ctxt =[-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1]
k =[-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1]
rcon=[0x01,0x02,0x04,0x08,0x10,0x20,0x40,0x80,0x1b,0x36]
def key_schedule_inv(key):
# encryption round keys
Ke = [[0] * 4 for i in range(11)]
# copy user material bytes into temporary ints
tk = []
for i in range(0, 4):
tk.append((ord(key[i * 4]) << 24) | (ord(key[i * 4 + 1]) << 16) |
(ord(key[i * 4 + 2]) << 8) | ord(key[i * 4 + 3]))
# copy values into round key arrays
for j in range(4):
Ke[j / 4][j % 4] = tk[j]
rconpointer = 10
for n in range(1,11):
# extrapolate using phi (the round key evolution function)
for i in range(4-1,0, -1):
tk[i] ^= tk[i-1]
rconpointer -= 1
tt = tk[3]
tk[0] ^= (Sbox[(tt >> 16) & 0xFF] & 0xFF) << 24 ^ \
(Sbox[(tt >> 8) & 0xFF] & 0xFF) << 16 ^ \
(Sbox[ tt & 0xFF] & 0xFF) << 8 ^ \
(Sbox[(tt >> 24) & 0xFF] & 0xFF) ^ \
(rcon[rconpointer] & 0xFF) << 24
# copy values into round key arrays
for j in range(4):
Ke[(j+(n*4)) / 4][(j+(n*4)) % 4] = tk[j]
return ''.join(["%08X" % k for k in Ke[10]])
def find_kb(b=1):
# We use same encoding st10:e_st10 for all bytes of the state
e_ctxt[b] = finalTable[b][e_st10]
# Guess k[b]
for k[b] in range(256):
ctxt[b] = Sbox[st10]^k[b]
if Ginv[e_ctxt[b]]!=ctxt[b]:
continue
if b < 15:
return (find_kb(b+1))
else:
return k
# finalTable implements for each ith byte x of the state G(kR10[i] ^ Sbox(X2_inv(x)))
# e_st10 = x = internally encoded state before round 10
# st10 = X2_inv(x) = plain state before round 10
# ctxt = kR10[i] ^ Sbox(X2_inv(x)) = plain ciphertext after round 10
# e_ctxt = G(kR10[i] ^ Sbox(X2_inv(x))) = externally encoded ciphertext after round 10
# Choose arbitrary first e_ctxt:
e_ctxt[0]=0
ctxt[0] = Ginv[e_ctxt[0]]
e_st10 = finalTable_inv[0][e_ctxt[0]]
# Guess first k[0] -> deduce the other bytes of the round-10 key
for k[0] in range(256):
st10 = Sbox_inv[ctxt[0]^k[0]]
kb=find_kb()
kR10=[kb[j/4 + j%4*4] for j in range(16)]
kAES=key_schedule_inv(''.join([chr(x) for x in kR10]))
# print 'kR10=',''.join(["%02X" % i for i in kR10]), '=> K=', kAES
aes = AES.new(kAES.decode('hex'), AES.MODE_ECB)
if aes.encrypt(pref)==cref:
print "FOUND!"
print 'kR10=',''.join(["%02X" % i for i in kR10]), '=> K=', kAES
print "Partial aes.xorTables[2] mapping: %02X:%02X " % (st10, e_st10)
FOUND! kR10= 66CA8706495D4543EAD87A31199E5889 => K= 4A7BB85DC1446AA1112222223B2A99FF Partial aes.xorTables[2] mapping: 9B:1D
This attack took 0.12s on my laptop.
Final word
The challenges were great, fun and educative!
The organizers did a great job to build them!
If I may suggest something to the organizers of the next edition: please change the rules.
First blood bonus work well for short CTFs (2-3 days) but for such long CTF (81.5 days!) it can become very frustrating: first blood bonuses were distributed quite fast, within 3 days I think, and then I sat in the uncomfortable situation where I was the first to finish all the challenges after 5.5 days and then had no choice but to watch the other participants playing for 76 days, till those who collected more first blood bonuses than I at the very beginning managed to complete all challenges and finally ended up above me. Hopefully only @hellmann1908 had enough bonuses to potentially threaten my position and indeed he eventually finished first (поздравления!!).
In the same spirit, till the very last moment the 2 participants who got one first blood bonus but didn't solve any other challenge could potentially jump ahead of the 5 participants who solved all challenges since a while but were not active in the very first hours of the challenge.
CTFs are fun, except when you can't play anymore but witness helplessly the others slowly overtaking you...
So I suggest to adapt the first blood rule for a next edition, e.g.:
- either by attributing also substantial first blood points to those who solve all challenges first
- or by dropping first blood mechanism and by weighting points with remaining days: a 10pts challenge solved the first day (80 days remaining) gives you 10*(80-1)=720pts; a 20pts challenge solved after 30 days gives you 20*(80-30)=1000pts, or similar mechanism to keep some incentive to solve the challenges as fast as possible during the entire competition.
For such long CTFs I like also the SSTIC rule: motivate people to submit a write-up and promote the best ones. So it will also be educational for those who didn't play the CTF but are eager to learn.
If you've comments, remarks, questions, suggestions, etc, you can contact me here or via Twitter @doegox