NSC Writeups
Oppida/NoSuchCon challenge
Intro
In April 2013, Oppida proposed a challenge associated with NoSuchCon 2013.
The challenge was designed by Eloi Vanderbéken @elvanderb and consisted into a PE binary embedding a white-box AES implementation.
It was of "keygen-me" type.
The challenge was broken by a few people and some write-ups are available:
- by Axel @0vercl0k: AES Whitebox Unboxing: No Such Problem
- by Arnaud @kutioo: NoSuchCon 2013 challenge - Write up and Methodology
- by Guy @Shiftreduce: Interactive deobfuscation (ppt)
To break the challenge one has to guess what input to the white-boxed AES will produce the desired output such that MD5(nickname) == AES(serial) i.e. to revert the AES block such that serial=AES^-1(MD5(nickname)).
This white-box being made of look-up tables, it could be reverted step by step, round by round from output to input, but the AES key itself was left unbroken.
There are pointers in Shiftreduce's presentation to the BGE attack, a now classical attack against a no less classical Chow white-box AES implementation but this implementation is quite different from Chow implementation and AFAIK Shiftreduce didn't recover the key.
Because I got curious about white-box only recently, I looked around what was publicly available and decided to investigate this one, a bit late for the competition I admit ;-)
The advantage of starting late is that I can rely on the wonderful work published by those three people and concentrate directly on the white-box itself, sparing me the need to peel the onion at first (it would have made me crying for sure).
After the challenge period, Eloi even published the code of his generator, very useful to study it and generate our own challenges (under Linux)!
Structure
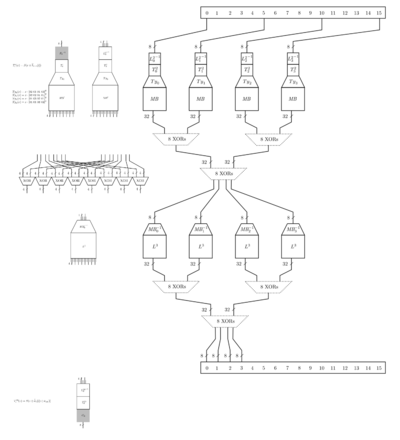
The drawing depicts the detail of the computation of one AES round, more precisely just the first byte of the state (and the three next, depending on the same 4 input bytes).
The first and last rounds are different:
- First round is similar to intern rounds but the tables applying the SBox here are also applying the initial round key in a so-called TBox and the input is not encoded by but by a so-called external encoding to be reverted.
- Last round as usual doesn't contain the MixColumn operation therefore is much simpler but another external encoding is applied on the output.
Notations of the drawing (please forgive my lack of math strictness):
All datapaths are 8-bit wide
- applies the inverse input encoding, a random 8-bit bijection
- applies the output encoding, a random 8-bit bijection
- is similar to Chow's but used only in first round
- is the AES SBox
- is multiplication by a single element of AES'MDS matrix
- is xoring by a share j of round r key byte i.
There are 4 shares therefore - for and apply an intermediate encoding, a random 8-bit bijection, and its inverse
- and apply an intermediate encoding, a random 8-bit bijection, and its inverse.
So encodes intermediate results between rounds. - is a byte xor 2x8-bit -> 8-bit
So this design makes use of 9 random substitution tables (that you don't find as such in the binary but which are used during generation) and their inverse:
and the same substitutions are re-used in all rounds (otherwise the 3 large xor tables would have to be duplicated many times)
At the end, the binary contains those tables:
- 3 xor tables of 256*256 values
- 9*16*4 round tables of 256 values
- 16 final round tables of 256 values
A curiosity of the design when compared with classical Chow is that each round key is applied before MixCol and therefore split into 4 random shares (recombined later by the xors). So the first round tables contain already the first two round keys.
If you want to compare with Chow, see A Tutorial on White-box AES by James A. Muir and zoom on this picture:
Attack
Because the internal encoding is the same between all rounds one may choose to attack a reduced version of AES with only 3 round keys but the problem is that the external encodings are completely unknown.
I propose another attack that works against any of the intermediate rounds and doesn't require a ton of equations because... I hate math.
Here attacking Round 3 but any round between 2 and 9 will do.
Let's guess the encoding of one single value in , the encoding table used between rounds.
Encoding of is : .
Try to find the corresponding key of 3nd round (so the 4rd round key):
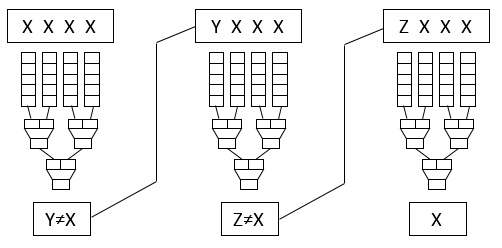
- There are 16 groups of round tables for each round, taking 4 bytes as input and producing one byte (one round table group here is actually the 4 sub-round tables combined with the 3 xor tables)
- To attack one group, we fix the 4 input bytes as so the decoded input is supposed to be
- We compute the encoded output byte out and compare it with
- if output , we create a new input and chain executions of that group till output so we know decoded output is
- The required number of iterations to reach an output is then compared with a clean implementation without encodings to check which k candidates require the same number of iterations, so here going from to
Example requiring 3 iterations:
Clean group implementation:
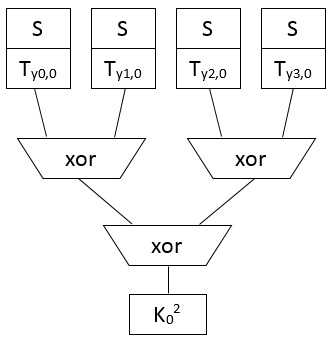
So from each initial encoding guess we get typically something like this: (i=ith byte, n=nr of iterations)
Hypothesis 00 is encoded as 00
i=00 n=10 k= 12 22 63 87 C5 D7 F0 F4
i=04 n=21 k= 05 63 F0 FA
i=08 n=E8 k= 1E 63 6D 78 A6 FE
i=12 n=0B k= 63
i=01 n=64 k= 00 05 22 23 63 A2 A9 BF C5 C9 D0 DF F1
i=05 n=7D k= 2E 63 70 97 AF
i=09 n=1E k= 04 05 36 54 63 A6 AF B7 C0 E7 EE FA
i=13 n=5A k= 2C 33 3B 3F 63 68 81 88 8F 94 A1 A3 AA CF DB ED F7
i=02 n=42 k= 42 63 74 D1
i=06 n=3D k= 63 73 A3
i=10 n=AC k= 0D 38 44 63 A6 E9
i=14 n=78 k= 07 1B 1E 33 45 57 61 63 68 88 8F 95 A3 AA B7 D1 DB ED F6 F7
i=03 n=D0 k= 0E 12 22 63 87 C5 D7 D8 F0 F4 FB
i=07 n=4A k= 02 63 8F A6
i=11 n=100 k= 0E 57 63 76 78 A6 E5 EA
i=15 n=E6 k= 11 33 4B 56 5A 63 6B 7A 8F 93 B1 ED
Then we can take a second guess for the encoding value of and filter the k candidates to keep those which are compatible with those we kept.
If no k candidates is left for one of the round key bytes, we backtrack our encoding guesses.
Here there is already no key candidate left.
So we backtrack and try another guess for the encoding of till...
Hypothesis 00 is encoded as CE
i=00 n=AE k= 18 63 70 72 74 77 7D 8D 9B
i=04 n=78 k= 04 05 2D 36 3F 40 46 54 63 78 89 8E 9B A6 AF B7 C0 CD E7 EE FA
i=08 n=E8 k= 1E 63 6D 78 A6 FE
i=12 n=F0 k= 07 1A 1B 1E 33 36 44 45 4C 57 5D 61 63 68 6F 88 8F 95 A3 AA B7 C5 D1 DB ED F6 F7 FC
i=01 n=EE k= 0B 41 4E 63 76 A8 BB CA DE EB
i=05 n=7D k= 2E 63 70 97 AF
i=09 n=1E k= 04 05 36 54 63 A6 AF B7 C0 E7 EE FA
i=13 n=100 k= 13 33 45 49 57 63 8F BF C5 C7 ED
i=02 n=47 k= 63 96
i=06 n=3D k= 63 73 A3
i=10 n=AC k= 0D 38 44 63 A6 E9
i=14 n=DF k= 30 63 F9
i=03 n=D8 k= 0A 12 17 22 34 4F 52 58 63 74 79 95 B7 C5 CF D7 E2 ED
i=07 n=B3 k= 63 9D A4
i=11 n=100 k= 0E 57 63 76 78 A6 E5 EA
i=15 n=78 k= 07 1B 1E 33 45 57 61 63 68 88 8F 95 A3 AA B7 D1 DB ED F6 F7
(in bold I already highlight the correct key bytes that we'll recover in a moment)
Hypothesis 01 is encoded as 10
i=00 n=28 k= 7D 9B
i=04 n=24 k= 2D CD
i=08 n=E8 k= 6D FE
i=12 n=67 k= 44
i=01 n=B0 k= 63 A8
i=05 n=7D k= 2E 70
i=09 n=82 k= 54
i=13 n=38 k= 13 C7
i=02 n=48 k= 96
i=06 n=3D k= A3
i=10 n=AC k= 0D 38 44
i=14 n=1C k= 30
i=03 n=6C k= 79
i=07 n=4A k= A4
i=11 n=100 k= 76 EA
i=15 n=44 k= 1B B7
Hypothesis 02 is encoded as A0
i=00 n=1E k= 9B
i=04 n=21 k= CD
i=08 n=E8 k= 6D FE
i=12 n=E8 k= 44
i=01 n=87 k= A8
i=05 n=36 k= 2E
i=09 n=82 k= 54
i=13 n=B3 k= 13
i=02 n=3B k= 96
i=06 n=11 k= A3
i=10 n=35 k= 0D
i=14 n=C8 k= 30
i=03 n=2F k= 79
i=07 n=4A k= A4
i=11 n=100 k= 76 EA
i=15 n=48 k= B7
And so on.
At the end only one possible key round is left so we found the round key and the complete mapping.
R3K candidate: 9BCD6D44A82E541396A30D3079A476B7
Then it's just a matter of reversing the key scheduling of AES (yes it's invertible) to go back to the first round key == AES key.
K00: 4E5343234F707069646123B8DCE442D0 K01: 267F33A5690F43CC0D6E6074D18A22A4 K02: 5AEC7A9B33E339573E8D5923EF077B87 K03: 9BCD6D44A82E541396A30D3079A476B7 <= K04: DAF5C4F272DB90E1E4789DD19DDCEB66 K05: 4C1CF7AC3EC7674DDABFFA9C476311FA K06: 979EDA0CA959BD4173E647DD34855627 K07: 402F1614E976AB559A90EC88AE15BAAF K08: 99DB6FF070ADC4A5EA3D282D44289282 K09: B6947CEBC639B84E2C049063682C02E1 K10: F1E384AE37DA3CE01BDEAC8373F2AE62
So the AES key is 4E5343234F707069646123B8DCE442D0 !
echo 4E5343234F707069646123B8DCE442D0|xxd -r -p NSC#Oppida#<some_garbage>
mapping:
00:CE 01'10 02:A0 03:48 04:C1 05:61 06:33 07:E4 08:6B 09:19 0A:C0 0B:E6 0C:C9 0D:6D 0E:93 0F:E1 10:EA 11:5F 12:13 13:EF 14:3C 15:07 16:54 17:02 18:CA 19:9F 1A:DF 1B:1E 1C:AA 1D:9B 1E:99 1F:03 20:DD 21:FF 22:B7 23:8F 24:37 25:EE 26:4F 27:F7 28:C5 29:81 2A:E5 2B:CF 2C:FB 2D:D5 2E:FD 2F:E3 30:7A 31:D3 32:41 33:C7 34:40 35:8C 36:CC 37:4C 38:26 39:30 3A:45 3B:C8 3C:F2 3D:56 3E:9D 3F:CD 40:D6 41:82 42:B5 43:6F 44:BB 45:1D 46:AF 47:67 48:F9 49:52 4A:6E 4B:DC 4C:BD 4D:59 4E:BA 4F:8B 50:18 51:22 52:7F 53:87 54:A8 55:35 56:A4 57:90 58:4D 59:57 5A:7C 5B:6C 5C:55 5D:24 5E:D8 5F:5B 60:C2 61:84 62:2D 63:11 64:9C 65:4E 66:28 67:68 68:F3 69:65 6A:E7 6B:89 6C:15 6D:2A 6E:01 6F:96 70:DE 71:C3 72:BC 73:E0 74:A3 75:63 76:E8 77:DB 78:B2 79:0D 7A:5D 7B:5A 7C:A6 7D:50 7E:F6 7F:D4 80:B1 81:5E 82:95 83:C4 84:78 85:4B 86:38 87:34 88:06 89:F8 8A:AE 8B:F1 8C:27 8D:71 8E:14 8F:B4 90:E2 91:49 92:2C 93:09 94:BE 95:7D 96:D7 97:4A 98:EC 99:70 9A:04 9B:2B 9C:92 9D:66 9E:9A 9F:32 A0:6A A1:97 A2:31 A3:9E A4:08 A5:3A A6:43 A7:85 A8:0C A9:91 AA:A2 AB:D1 AC:8E AD:20 AE:AC AF:A5 B0:39 B1:74 B2:B6 B3:16 B4:76 B5:F4 B6:3D B7:5C B8:1A B9:ED BA:51 BB:0B BC:80 BD:2F BE:1C BF:DA C0:94 C1:A9 C2:12 C3:05 C4:73 C5:0A C6:53 C7:62 C8:AD C9:F5 CA:3F CB:75 CC:25 CD:77 CE:B9 CF:42 D0:36 D1:7E D2:EB D3:BF D4:B0 D5:E9 D6:C6 D7:98 D8:69 D9:72 DA:60 DB:B8 DC:86 DD:23 DE:47 DF:00 E0:88 E1:B3 E2:83 E3:FC E4:64 E5:46 E6:A7 E7:CB E8:D2 E9:58 EA:7B EB:21 EC:F0 ED:44 EE:3B EF:3E F0:0E F1:1B F2:17 F3:FA F4:2E F5:D9 F6:8D F7:AB F8:0F F9:D0 FA:1F FB:FE FC:A1 FD:29 FE:8A FF:79
The full attack takes 3.1s on my laptop.
Recovery of the external encodings is left as exercise for the reader ;-)
Fun facts: if on the clear implementation we don't look for to but for to where is arbitrarily chosen, we still find the right round key but with a wrong mapping.
Thanks for your patience if you have read so far, feel free to share your thoughts with me (@doegox).
And thanks to Eloi for this great challenge and to Axel, Arnaud and Guy those who have shared their write-up!
Epilogue
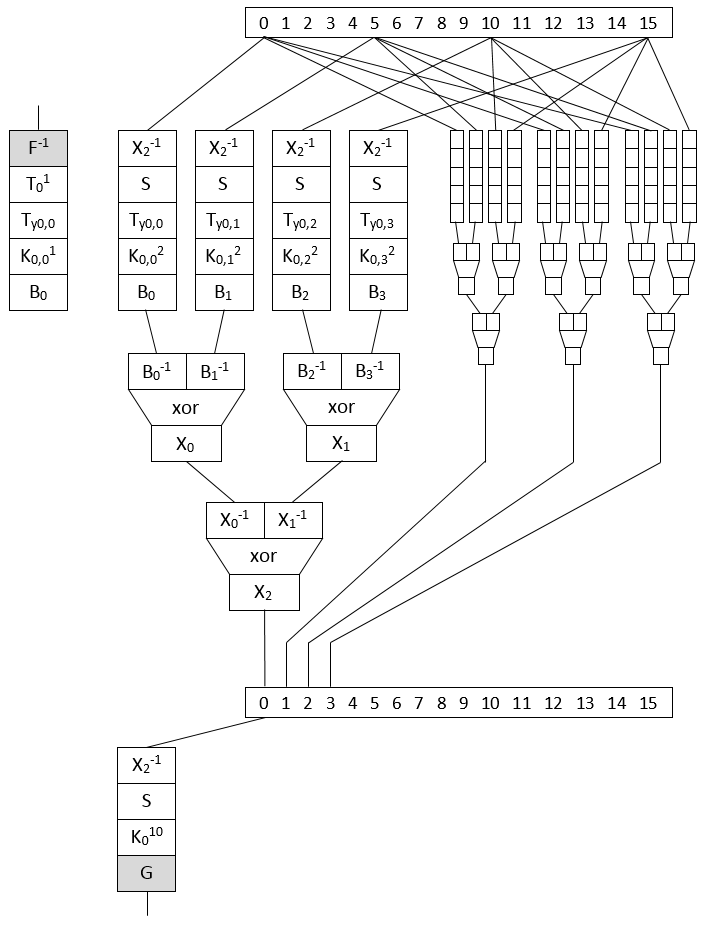
Before being able to mount the attack, we had to recover the actual tables and that's not that simple.
Axel's version contains the tables but still unsorted as this was not needed for him to break the challenge:
- Table names and positions are random
- Code is flattened
- Intermediate variables are taken in arbitrary order from a reusable pool, including output buffer
- Steps are calculated out of order, only order due to dependencies is preserved
- Half of tables are actually tables to function snippets in the original code but Axel's version removed already that obfuscation layer, sigh!
So to rename properly the tables one needs to:
- Rewrite code with static single assignment (SSA) form, to be able to reorder it without conflicts
- Start from output buffers and rename logically intermediate values and tables
Detailed steps:
- As SSA version I took wbaes128_solve.cpp from his writeup, extracted and reordered the rounds (by hand)
//ROUND1 memory[2] = T_00430909[key[0x0]]; memory[9] = T_004E19C5[key[0xa]]; memory[10] = T_0055BF00[key[0xf]]; memory[18] = TH_005D3C2C[key[0xf]]; memory[20] = T16_00415EFE[memory[9]][memory[10]]; etc
- To have something to compare with, I took the whitebox generator and replaced actual lookups by printf(), making sure all intermediate values are on SSA form too
b1_0[0] = rT0[0][0][t[0][0]] b1_0[1] = rT0[0][1][t[0][5]] b1_0[2] = rT0[0][2][t[0][10]] b1_0[3] = rT0[0][3][t[0][15]] b1_0_01 = xT0[b1_0[0]][b1_0[1]] b1_0_23 = xT1[b1_0[2]][b1_0[3]] t[1][0] = xT2[b1_0_01][b1_0_23] etc
- Then I build a dictionary associating tables and indexes with each variable assignment from this output.
- Reading backward the SSA version, now I can make matches between table names:
fT[0] = TH_0049CA9E fT[1] = T_00493D6C fT[2] = TH_004866A5 fT[3] = T_005D1023 fT[4] = T_00534D4A ... rT0[0][0] = T_00438C5E rT0[0][1] = T_005FCF50 rT0[0][2] = TH_004D3B58 rT0[0][3] = TH_005D3C2C ...
- Then based on those matches, I generate C code to copy NSC tables to aes_wbs_s struct of the wb generator code
memcpy(aes.finalTable[0], TH_0049CA9E, sizeof(TH_0049CA9E)); memcpy(aes.finalTable[1], T_00493D6C, sizeof(T_00493D6C)); memcpy(aes.finalTable[2], TH_004866A5, sizeof(TH_004866A5)); memcpy(aes.finalTable[3], T_005D1023, sizeof(T_005D1023)); memcpy(aes.finalTable[4], T_00534D4A, sizeof(T_00534D4A)); ... memcpy(aes.roundTables[0][0][0], T_00438C5E, sizeof(T_00438C5E)); memcpy(aes.roundTables[0][0][1], T_005FCF50, sizeof(T_005FCF50)); memcpy(aes.roundTables[0][0][2], TH_004D3B58, sizeof(TH_004D3B58)); memcpy(aes.roundTables[0][0][3], TH_005D3C2C, sizeof(TH_005D3C2C)); ...
- Compile and execute :) We obtain a file with the right tables in the same format as the one produced by the whitebox generator code.
Source code
All scripts have finally been published here: https://github.com/SideChannelMarvels/Deadpool/tree/master/wbs_aes_nsc2013





![{\displaystyle T_{i}^{1}(x)=S(x\oplus {\hat {k^{0}}}[i])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/60cb416b0dbb752bd7c2f44f4ae7a31abb2d8df2)



![{\displaystyle K_{i,j}^{r}(x)=x\oplus {\hat {k_{j}^{r}}}[i]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/85408f77575837d0fd9612444e7e0c23bcdf1560)
![{\displaystyle {\hat {k^{r}}}[i]={\hat {k_{0}^{r}}}[i]\oplus {\hat {k_{1}^{r}}}[i]\oplus {\hat {k_{2}^{r}}}[i]\oplus {\hat {k_{3}^{r}}}[i]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e69cee89268f00289089abee425b544ba206a94)




















